Cho hai đường thẳng d 1 và d 2 song song với nhau. Trên d 1 có 10 điểm phân biệt, trên d 2 có n điểm phân biệt ( n ≥ 2 ). Biết có 2800 tam giác có đỉnh là các điểm nói trên. Tìm n?
A. 16
B. 21
C. 30
D. 20
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tam giác cần lập thuộc hai loại
Loại 1: Tam giác có một đỉnh thuộc d1 và hai đỉnh thuộc d2. Loại này có ![]() tam giác.
tam giác.
Loại 2: Tam giác có một đỉnh thuộc d2 và hai đỉnh thuộc d1. Loại này có ![]() tam giác.
tam giác.
Theo bài ra ta có: ![]()
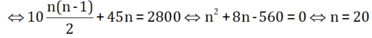
Chọn A.

Có 2 trường hợp sau:
+ Lấy 1 điểm trên d1 và 2 điểm trên d2, suy ra cớ 10 C n 2 tam giác
+ Lấy 2 điểm trên d1 và 1 điểm trên d2, suy ra cớ n C 10 2 tam giác
Suy ra có
![]()

Đáp án B
Có 2 trường hợp sau:
+ Lấy 1 điểm trên d1 và 2 điểm trên d2, suy ra cớ 10 C n 2 tam giác
+ Lấy 2 điểm trên d1 và 1 điểm trên d2, suy ra cớ n C 10 2 tam giác
Suy ra có
![]()

Chọn đáp án D
Một điểm bất kì trên đường thẳng d1 với hai điểm phân biệt trên d2 hoặc cứ một điểm bất kì trên đường thẳng d2 với hai điểm phân biệt trên d1 tạo thành một tam giác.
Vậy tổng sổ tam giác thỏa mãn đề bài là ![]()
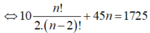
![]()
![]()
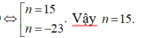
Tam giác cần lập thuộc hai loại
Loại 1: Tam giác có một đỉnh thuộc d 1 và hai đỉnh thuộc d 2 .
Loại này có C 10 1 . C n 2 tam giác.
Loại 2: Tam giác có một đỉnh thuộc d 2 và hai đỉnh thuộc d 1 .
Loại này có C 10 2 . C n 1 tam giác.
Theo bài ra ta có: C 10 1 . C n 2 + C 10 2 . C n 1 = 2800
⇔ 10 n ( n − 1 ) 2 + 45 n = 2800 ⇔ n 2 + 8 n − 560 = 0 ⇔ n = 20
Chọn đáp án D