Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án D
Xét hàm số y = f x = 2 x 4 - 3 x 2 + m trên - 1 2 ; 2 .
Ta có f ' x = 8 x 3 - 6 x , ∀ x ∈ - 1 2 ; 2
Phương trình f ' x = 0 ⇔ - 1 2 ≤ x ≤ 2 4 x 3 - 3 x = 0 ⇔ [ x = 0 x = 3 2
Tính giá trị f 0 = m ; f - 1 2 = m - 5 8 f 2 = m + 20 ; f 3 2 = m - 9 8
Khi đó giá trị nhỏ nhất của hàm số f(x) là m - 9 8 = 31 8 ⇔ m = 5
Chọn đáp án C
Phương pháp
Số nghiệm của phương trình f(x)=m là số giao điểm của đồ thị hàm số y=f(x) và y=m song song với trục hoành.
Cách giải
Ta có:
Số nghiệm của phương trình f(x)=m là số giao điểm của đồ thị hàm số y=f(x) và y=m+1 song song với trục hoành.
Từ BBT ta thấy để phương trình f(x)-1=m có đúng 2 nghiệm thì
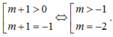
Đạo hàm f'(x) = m 2 - m + 1 ( x + 1 ) 2 > 0, ∀ x ∈ [ 0 ; 1 ]
Suy ra hàm số f(x) đồng biến trên [0; 1] nên min f(x) = f(0) = -m2+m
Theo bài ta có:
-m2+ m= -2 nên m= -1 hoặc m= 2.
Chọn D.
Điều kiện : x≠ -m.
+ Ta có: y ' = x 2 + 2 m x + m 2 - 1 ( x + m ) 2 = ( x + m ) 2 - 1 ( x + m ) 2
y ' = 0 ↔ ( x + m ) 2 = 1 ↔ x = 1 - m > - m ∨ x = - 1 - m < - m
+ Do hệ số x2 là số dương và theo yêu cầu đề bài ta có bảng biến thiên như sau:
+ Hàm số đạt giá trị nhỏ nhất tại x0=1-m ∈ (0; 2) nên 0< -m+1 < 2
Hay -1< m< 1.
+ Kết hợp điều kiện để hàm số liên tục trên [0; 2] thì
Ta được 0<m<1
Chọn A