Cho tứ diện ABCD. Gọi G 1 và G 2 lần lượt là trọng tâm các tam giác BCD và ACD. Khẳng định nào sau đây là sai?
A. G 1 G 2 //(ABD)
B. G 1 G 2 //(ABC)
C. B G 1 , A G 2 và CD đồng quy
D. G 1 G 2 = 2 3 A B
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A.
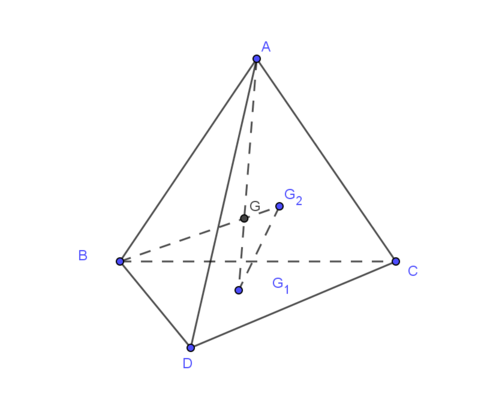
Hình vẽ dễ thấy tính song song là: G 1 G 2 ∥ A B
Chứng minh
Vì G G 1 G A = G G 2 G B = 1 4 ⇒ G 1 G 2 ∥ A B

Gọi E là trung điểm của AB, M, N lần lượt là trọng tâm của các tam giác ABC, ABD nên:
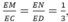
Theo định lí Ta – lét ta có: MN // CD. Vậy MN // (BCD), MN // (ACD).
Đáp án C.
Gọi N là trung điểm của CD
● Khi đó A, G 2 , N thẳng hàng và B, G 1 , N thẳng hàng.
Do đó, B G 1 , A G 2 và CD đồng quy
Do đó D sai. Chọn D.