Question

[Pham Trong Bach]

Cho hàm số f x = x  . Để tính f '(0), bạn Thảo Huyền đã trình bày lời giải trên bảng theo các bước sau

Bước 1: f x = x = x x > 0 0 x = 0 - x x < 0  

Bước 2:

f ' 0 + = lim x → 0 + f x - f 0 x - 0 = lim x → 0 + x - 0 x - 0 = 1  

Bước 3: 

f ' 0 - = lim x → 0 - f x - f 0 x - 0 = lim x → 0 - x - 0 x - 0 = 1

Bước 4:  f ' 0 + = f ' 0 - = 1

Vậy f ' (0) = 1

Sau khi quan sát trên bảng, bạn Duy Lĩnh đã phát hiện ra rằng trong lời giải của bạn Thảo Huyền có một bước bị sai sót. Vậy sai sót đó từ bước nào?

A. Bước 1

B.Bước 2

C. Bước 3

D. Bước 4

Answer 1

[Cao Minh Tâm]

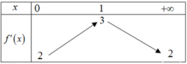
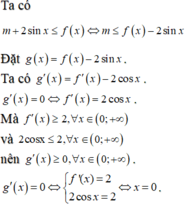
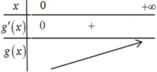
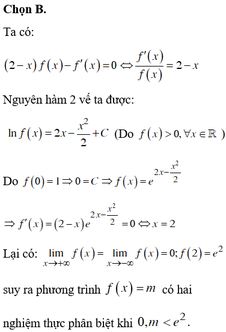
Sai từ bước 3 bởi vì  

f ' 0 - = lim x → 0 - f x - f 0 x - 0 = lim x → 0 - - x - 0 x - 0 = 1

Do f ' 0 + ≠ f ' 0 -  nên f '(0) không tồn tại

Đáp án C