Tìm các nghiệm x ∈ 0 ; π 2 của phương trình sau
4 sin 2 π - x 2 - 3 π 2 - 2 x = 1 + 2 cos 2 x - 3 π 4
A. x = 5 π 8
B. x ∈ 5 π 18 ; 7 π 18
C. x = 7 π 18
D. x ∈ ∅
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Δ=(4m+3)^2-4*2*(2m^2-1)
=16m^2+24m+9-16m^2+8
=24m+17
Để phương trình có hai nghiệm phân biệt thì 24m+17>0
=>m>-17/24
b: Để phương trìh có nghiệm kép thì 24m+17=0
=>m=-17/24
c: Để phương trình vô nghiệm thì 24m+17<0
=>m<-17/24

Lời giải:
a) Để 2 pt cùng có nghiệm thì:
\(\left\{\begin{matrix} \Delta'_1=16-4m\geq 0\\ \Delta_2=1+16m\geq 0\end{matrix}\right.\Leftrightarrow 4\geq m\geq \frac{-1}{16}\)
b)
Gọi $2a,a$ lần lượt là nghiệm của PT $(1)$ và PT $(2)$:
Ta có:
\(\left\{\begin{matrix} (2a)^2-8.2a+4m=0\\ a^2+a-4m=0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} a^2-4a+m=0\\ a^2+a-4m=0\end{matrix}\right.\)
\(\Rightarrow 5a=5m\Leftrightarrow a=m\)
Thay vô: $m^2+m-4m=0\Leftrightarrow m^2-3m=0$
$\Leftrightarrow m=0$ hoặc $m=3$

Bài 2:
Để phương trình có hai nghiệm trái dấu thì (m-2)(m+2)<0
hay -2<m<2

a: \(\Leftrightarrow\left(2m-4\right)^2-4\left(m^2-3\right)>=0\)
\(\Leftrightarrow4m^2-16m+16-4m^2+12>=0\)
=>-16m>=-28
hay m<=7/4
b: \(\Leftrightarrow16m^2-4\left(2m-1\right)\left(2m+3\right)=0\)
\(\Leftrightarrow16m^2-4\left(4m^2+4m-3\right)=0\)
=>4m-3=0
hay m=3/4
c: \(\Leftrightarrow\left(4m-2\right)^2-4\cdot4\cdot m^2< 0\)
=>-16m+4<0
hay m>1/4

Ta có: x − 3 x − 2 ≥ 0
Điều kiện: x ≥ 2
Bất phương trình tương đương là x − 3 ≥ 0 x − 2 = 0 ⇔ x ≥ 3 x = 2
Vậy tập nghiệm của bất phương trình là S = { 2 } ∪ [3;+ ∞ )

Ta có: ( x - 3 ) ( x - 2 ) ≥ 0
Điều kiện: x ≥ 2
Bất phương trình tương đương là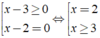
Vậy tập nghiệm của bất phương trình là x = 2 hoặc x ≥ 3

Thay x = −1 vào phương trình:
(−1)2 – 2(3m + 2).(−1) + 2m2 – 3m – 10 = 0
⇔ 2m2 + 3m – 5 = 0 ⇔ (2m + 5)(m – 1) = 0
m = − 5 2 ( L ) m = 1 ( N )
+) Với m = 1 ta có phương trình x2 – 10x – 11 = 0
⇔ (x – 11)(x + 1) = 0 ⇔ x = 11 x = − 1
Vậy nghiệm còn lại của phương trình là x = 11
Đáp án cần chọn là: A
Ta có:
4 sin 2 π - x 2 - 3 π 2 - 2 x = 1 + 2 cos 2 x - 3 π 4 ⇔ 2 1 - cos 2 π - x - 3 cos 2 x = 1 + 1 + cos 2 x - 3 π 2 ⇔ 2 - 2 cos x - 3 cos 2 x = 2 - sin 2 x ⇔ sin 2 x - 3 cos 2 x = 2 cos x ⇔ 1 2 sin 2 x - 3 2 cos 2 x = cos x ⇔ sin 2 x - π 3 = cos π 3 - x ⇔ x = 5 π 8 + k 2 π 3 x = 5 π 6 + k 2 π
Vì x ∈ 0 ; π 2 nên ta chọn được nghiệm x = 5 π 8
Đáp án A