Cho hai tập hợp M = { 8 k + 5 | k ∈ ℤ } , N = { 4 l + 1 | l ∈ ℤ } .
Khẳng định nào sau đây là đúng?
A. M ⊂ N
B. N ⊂ M
C. M = N
D. M = ∅ , N = ∅
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án: B
2 x x 2 + 1 ≥ 1 ⇔ 2 x - x 2 - 1 x 2 + 1 ≥ 0 ⇔ 2 x - x 2 - 1 ≥ 0 ⇔ - ( x - 1 ) 2 ≥ 0 ⇔ x = 1 ⇒ A = { 1 } .
∆ ' = b 2 - 4 . Để phương trình vô nghiệm thì
∆ ' < 0 ⇔ b 2 - 4 < 0 ⇔ b 2 < 4 ⇔ - 2 < b < 2 ⇒ B = { - 1 ; 0 ; 1 } . ⇒ A ⊂ B .

Vì z 1 = 1 + 2 i là nghiệm phương trình z 2 + b z + c = 0 nên
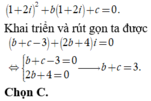

Đáp án A.
Ta có:
x − 3 x 2 − 2 x + 1 = x − 1 − 2 x − 1 2 = 1 x − 1 − 2 x − 1 2 ⇒ ∫ x − 3 x 2 − 2 x + 1 d x = ∫ 1 x − 1 − 2 x − 1 2 d x

Đáp án B
TXĐ của hàm y = tanx là D = ℝ \ π 2 + k π | k ∈ ℤ nên TXĐ của hàm y = tan 2 x là D = ℝ \ π 4 + k π 2 | k ∈ ℤ
TXĐ của hàm y = cot x là D = ℝ \ k π | k ∈ ℤ nên TXĐ của hàm y = cot 2 x là D = ℝ \ k π 2 | k ∈ ℤ