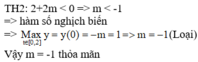Cho hình chữ nhật ABCD và số thực k >0. Tập hợp các điểm M thỏa mãn đẳng thức M A → + M B → + M C → + M D → = k là
A. một đoạn thẳng.
B. một đường thẳng.
C. một đường tròn.
D. một điểm.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
6 tháng 2 2017
Đúng(0)
Những câu hỏi liên quan
CM
30 tháng 10 2017
Gọi I là tâm của hình chữ nhật ABCD ta có 2 M I → = M A → + M C → 2 M I → = M B → + M D → , ∀ M .
Do đó :
M A → + M B → + M C → + M D → = k ⇔ ( M A → + M C → ) + ( M B → + M D → ) = k ⇔ 2 M I → + 2 M I → = k ⇔ 4 M I → = k ⇔ M I → = k 4 . ( * )
Vì I là điểm cố định nên tập hợp các điểm M thỏa mãn đẳng thức (*) là đường tròn tâm I bán kính R = k 4 .
Chọn C.
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 10 2019
Gọi O là tâm hình chữ nhật
\(\left|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}+\overrightarrow{MD}\right|=k\)
\(\Leftrightarrow\left|\overrightarrow{MO}+\overrightarrow{OA}+\overrightarrow{MO}+\overrightarrow{OB}+\overrightarrow{MO}+\overrightarrow{OC}+\overrightarrow{MO}+\overrightarrow{OD}\right|=k\)
\(\Leftrightarrow4\left|\overrightarrow{MO}\right|=k\)
\(\Rightarrow\left|\overrightarrow{MO}\right|=\frac{k}{4}\Rightarrow\) M thuộc đường tròn tâm O bán kính \(\frac{k}{4}\)
CM
13 tháng 9 2018
Chọn B
Cách giải: Ta có:
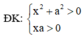
log 2 x 2 + a 2 + log 2 x 2 + a 2 + log 2 x 2 + a 2 + . . . + log . . . 2 ⏝ n c ă n x 2 + a 2 - 2 n + 1 - 1 log 2 x a + 1 = 0
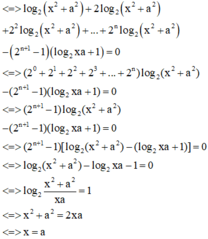
