Cho hai đường tròn bằng nhau (O;R) và (O’;R) với tâm O và O’ phân biệt. có bao nhiêu phép vị tư biến (O;R) thành (O’;R) ?
A. Không có phép vị tự nào
B. Có một phép vị tự duy nhất
C. Chỉ có hai phép vị tự
D. Có vô số phép vị tự
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

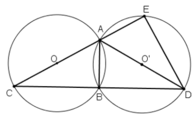
Vì A,B,C ∈ (O)
⇒ BO = OA = OC
⇒ BO = AC/2.
Tam giác ABC có đường trung tuyến BO và BO bằng một phần hai độ dài cạnh tương ứng AC
=> Tam giác ABC là tam giác vuông tại B ( định lí)
⇒ 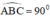
Chứng minh tương tự
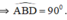
Đường tròn tâm O và O’ bằng nhau ⇒ AC = AD.(AC,AD lần lượt là bán kính của (O) và (O’))
Xét hai tam giác vuông ΔABC và ΔABD có:
AB chung, AC = AD
⇒ ΔABC = ΔABD (cạnh huyền – cạnh góc vuông)
⇒ BC = BD(hai cạnh tương ứng)
⇒ 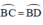 ( định lý )
( định lý )

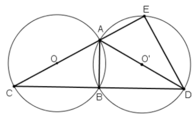
Xét tam giác AED có đường trung tuyến EO' bằng một phần hai cạnh tương ứng là AD ( O'E = O'A = O'D = AD/2)
=> Tam giác AED vuông tại E
⇒ 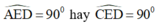
⇒ ΔECD vuông tại E.
Tam giác ECD vuông có EB là đường trung tuyến ứng với cạnh huyền( Vì BC = BD câu (a) )
⇒ EB = BD (CD/2).
⇒ 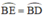 (định lý) hay B là điểm chính giữa cung
(định lý) hay B là điểm chính giữa cung 

Hai cung lớn 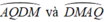 có số đo bằng nhau.
có số đo bằng nhau.
* Chú ý : Phân biệt : so sánh hai cung và số đo hai cung.
So sánh hai cung trong trường hợp hai cung trong một đường tròn hoặc trong hai đường tròn có bán kính bằng nhau.
Còn so sánh số đo hai cung : ta luôn so sánh được.

Các cung nhỏ có số đo bằng nhau là:
Trong đường tròn lớn:
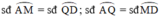
Trong đường tròn nhỏ:
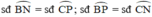

Các cung nhỏ có số đo bằng nhau là:
Trong đường tròn lớn:
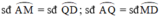
Trong đường tròn nhỏ:
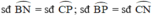

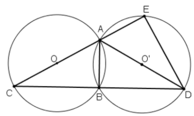
a) Vì A,B,C ∈ (O)
⇒ BO = OA = OC
⇒ BO = AC/2.
Tam giác ABC có đường trung tuyến BO và BO bằng một phần hai độ dài cạnh tương ứng AC
=> Tam giác ABC là tam giác vuông tại B ( định lí)
⇒ 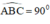
Chứng minh tương tự
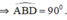
Đường tròn tâm O và O’ bằng nhau ⇒ AC = AD.(AC,AD lần lượt là bán kính của (O) và (O’))
Xét hai tam giác vuông ΔABC và ΔABD có:
AB chung, AC = AD
⇒ ΔABC = ΔABD (cạnh huyền – cạnh góc vuông)
⇒ BC = BD(hai cạnh tương ứng)
⇒ 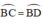 ( định lý )
( định lý )
b) Xét tam giác AED có đường trung tuyến EO' bằng một phần hai cạnh tương ứng là AD ( O'E = O'A = O'D = AD/2)
=> Tam giác AED vuông tại E
⇒ ![]()
⇒ ΔECD vuông tại E.
Ta có:
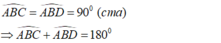
Suy ra: C, B, D thẳng hàng.
Tam giác ECD vuông có EB là đường trung tuyến ứng với cạnh huyền( Vì BC = BD câu (a) )
⇒ EB = BD (CD/2).
⇒ 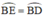 (định lý) hay B là điểm chính giữa cung
(định lý) hay B là điểm chính giữa cung 
Kiến thức áp dụng
+ Với hai cung nhỏ trong cùng một đường tròn hoặc hai đường tròn bằng nhau thì hai dây bằng nhau căng hai cung bằng nhau.

Vẽ lục giác đều ngoại tiếp đường tròn tâm O. Khi đó 6 đường tròn cần vẽ chính là các đường tròn nội tiếp các tam giác tạo thành từ O với 2 đỉnh kề nhau của lục giác ngoại tiếp đó.
Và ta có mỗi tam giác đó là tam đều nên tâm của 6 tam giác nhỏ chính là trọng tâm của các tam giác đều đó. Khi đó bán kính của 6 tam giác đó:
\(R=\frac{1}{3}.Ro=\frac{1}{3}.9=3\)
Qua phép vị tự tỉ số k biến đường tròn (O; R) thành (O’; R).
Ta có: R’ = R nên |k| = 1
Suy ra: k = 1 hoặc k = -1
* Nếu k= 1 thì phép tự là phép đồng nhất: ( mâu thuẫn giả thiết)
* Khi k=-1 thì tâm vị tự là trung điểm của OO’.
Đáp án B