Số gia của hàm số f(x) = x 3 ứng với x 0 = 2 và ∆ x = 1 bằng bao nhiêu?
A. -19
B. 7
C. 19
D. -7
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
26 tháng 7 2019
Đáp án C
- Ta có : x 0 + Δ x = 2 + 1 = 3 .
- Do đó, số gia của hàm số đã cho là:
1 tháng 9 2021
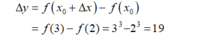
1.
\(A=\left\{1,2,3,4,5\right\}\)
\(A=\left\{x\in N^{\circledast}|x\le5\right\}\)
2.
a)Số phần tử là: \(\left(51-13\right)\div2+1=20\)( p/t)
b)Số phần tử là: \(\left(39-8\right)+1=32\)( p/t)
c)Số phần tử là vô cực
d)Số phần tử là 1
KN
4 tháng 7 2019
\(C=-\left|x+\frac{4}{7}\right|+\frac{12}{19}\)
Ta có: \(\left|x+\frac{4}{7}\right|\ge0\)nên \(-\left|x+\frac{4}{7}\right|\le0\)
\(\Rightarrow C=-\left|x+\frac{4}{7}\right|+\frac{12}{19}\le\frac{12}{19}\)
\(\Rightarrow C_{max}=\frac{12}{19}\)
(Dấu "="\(\Leftrightarrow x=\frac{-4}{7}\))
KN
4 tháng 7 2019
\(D=\left|x-\frac{5}{7}\right|+\frac{2}{3}\)
Vì \(\left|x-\frac{5}{7}\right|\ge0\)nên \(D=\left|x-\frac{5}{7}\right|+\frac{2}{3}\ge\frac{2}{3}\)
\(\Rightarrow D_{min}=\frac{2}{3}\)
(Dấu "="\(\Leftrightarrow x=\frac{5}{7}\))
CM
16 tháng 12 2018
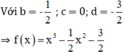
a) f’(x) = 3x2 – x.
⇒ f’(-1) = 4; f(-1) = -3.
⇒ Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ x = -1 là:
y = 4.(x + 1) – 3 = 4x + 1.
b) f’(sin x) = 0
⇔ 3.sin2x – sin x = 0
⇔ sin x.(3sin x – 1) = 0
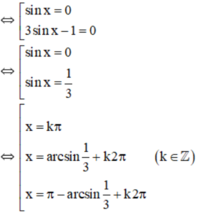
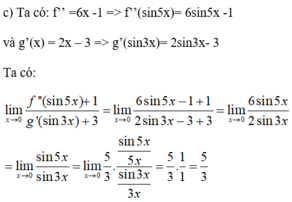
Đáp án C
Gọi Δ x là số gia của đối số; Δ y là số gia của hàm số. Ta có:
Δ y = f ( x 0 + Δ x ) − f ( x 0 ) = f ( 2 + 1 ) − f ( 2 ) = f ( 3 ) − f ( 2 ) = 3 3 − 2 3 = 19