Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án A
Phương pháp:
Dựa vào khái niệm cực trị và các kiến thức liên quan.
Cách giải:
(1) chỉ là điều kiện cần mà không là điều kiện đủ.
VD hàm số y = x3 có y' = 3x2 = 0 ⇔ x = 0. Tuy nhiên x = 0 không là điểm cực trị của hàm số.
(2) sai, khi f''(x0) = 0, ta không có kết luận về điểm x0 có là cực trị của hàm số hay không.
(3) hiển nhiên sai.
Vậy (1), (2), (3): sai; (4): đúng
A. Đúng (theo định nghĩa đạo hàm tại một điểm).
B. Đúng vì:
C. Đúng vì:
Chọn D
Đáp án D
- A. Đúng (theo định nghĩa đạo hàm tại một điểm).
- B. Đúng vì:
- C. Đúng vì:
+ Đặt:
Đáp án A
Mệnh đề 1) sai vì f ' x 0 = 0 chỉ là điều kiện cần chưa là điều kiện đủ để hàm số đạt cực trị tại x 0
Mệnh đề 2) Sai vì khi f ' x 0 = f ' ' x 0 = 0 có thể hàm số có thể đạt cực trị hoặc không đạt cực trị tại x 0 .
Mệnh đề 3) sai vì f ' x đổi dấu qua điểm x 0 thì điểm x 0 có thể là điểm cực đại hoặc điểm cực tiểu của hàm số.
Mệnh đề 4) Sai vì trong trường hợp này x 0 là điểm cực tiểu của đồ thị hàm số.
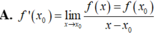
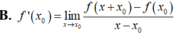
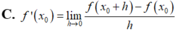
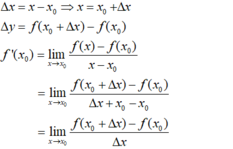
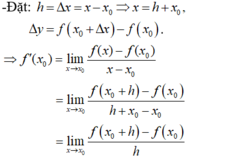
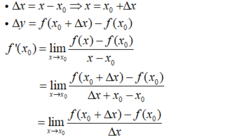
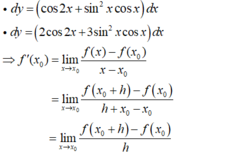
+ Nếu hàm số y= f(x) có đạo hàm tại điểm x0 thì hàm số sẽ liên tục tại điểm x0
+ Ngược lại, nếu hàm số liên tục tại điểm x0 thì chưa chắc hàm số đã có đạo hàm tại điểm x0.
+ Theo định nghĩa đạo hàm tại 1 điểm ta có:
f ' ( x 0 ) = lim x → x 0 f ( x ) − f ( x 0 ) x − x 0 và f ' ( x 0 ) = lim Δ x → 0 f ( x 0 + Δ x ) − f ( x 0 ) Δ x
Vậy D sai
Chọn D.