CÁC BẠN GIẢI JUP MIK VỚI !! :))
Bài 1: Xét tính đúng sai của các mệnh đề sau:
a) Phương trình có hai nghiệm phân biệt.
b) 2k là số chẵn. (k là số nguyên bất kì)
c) 211 – 1 chia hết cho 11.
Bài 2: Cho tứ giác ABDC: Xét hai mệnh đề
P: Tứ giác ABCD là hình vuông.
Q: Tứ giác ABCD là hình chữ nhật có hai đường chéo bằng vuông góc với nhau.
Hãy phát biểu mệnh đề P ↔ Q bằng hai cách khác nhau, xét tính đúng sai của các mệnh đề đó.
Bài 3: Cho mệnh đề chứa biến P(n): n2 – 1 chia hết cho 4 với n là số nguyên. Xét tính đúng sai của mệnh đề khi n = 5 và n = 2.
Bài 4: Nêu mệnh đề phủ định của các mệnh đề sau:

Bài 5: Xét tính đúng sai và nêu mệnh đề phủ định của các mệnh đề:
a) Tứ giác ABCD là hình chữ nhật.
b) 16 là số chính phương.

Bài 6: Cho tứ giác ABCD và hai mệnh đề:
P: Tổng 2 góc đối của tứ giác bằng 1800;
Q: Tứ giác nội tiếp được đường tròn.
Hãy phát biểu mệnh đề kéo theo P => Q và xét tính đúng sai của mệnh đề này.
Bài 7: Cho hai mệnh đề
P: 2k là số chẵn.
Q: k là số nguyên
Hãy phát biểu mệnh đề kéo theo và xét tính đúng sai của mệnh đề.
Bài 8: Hoàn thành mệnh đề đúng:
Tam giác ABC vuông tại A nếu và chỉ nếu ...................
- Viết lại mệnh đề dưới dạng một mệnh đề tương đương.
Bài 9: Xét tính đúng sai của các mệnh đề và viết mệnh đề phủ định của các mệnh đề.

Bài 10: Xét tính đúng sai của các suy luận sau: (mệnh đề kéo theo)

Bài 11: Phát biểu điều kiện cần và đủ để một:
- Tam giác là tam giác cân.
- Tam giác là tam giác đều.
- Tam giác là tam giác vuông cân.
- Tam giác đồng dạng với tam giác khác cho trước.
- Phương trình bậc 2 có hai nghiệm phân biệt.
- Phương trình bậc 2 có nghiệm kép.
- Số tự nhiên chia hết cho 2; cho 3; cho 5; cho 6; cho 9 và cho 11.
Bài 12: Chứng mình rằng: Với hai số dương a, b thì a + b ≥ 2√ab.
Bài 13: Xét tính đúng sai của mệnh đề:
Nếu một số tự nhiên chia hết cho 15 thì chia hết cho cả 3 và 5.
Bài 14: Phát biểu và chứng minh định lí sau:
a) n là số tự nhiên, n2 chia hết cho 3 thì n cũng chia hết cho 3.
b) n là số tự nhiên, n2 chia hết cho 6 thì n cũng chia hết cho cả 6; 3 và 2.
(Chứng minh bằng phản chứng)




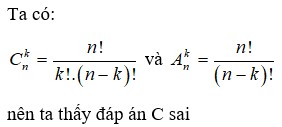

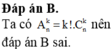
Đáp án là C. Ta có a,b∈N* không suy ra a -1, b -1∈N* . Do vậy không áp dụng được giả thiết quy nạp cho cặp {a -1, b -1}.
Chú ý: nêu bài toán trên đúng thì ta suy ra mọi số tự nhiên đều bằng nhau. Điều này là vô lí.