Cho hai số phức z1; z2 khác 0 thỏa mãn ![]() .Gọi A; B lần lượt là các điểm biểu diễn cho số phức z1; z2. Khi đó tam giác OAB là:
.Gọi A; B lần lượt là các điểm biểu diễn cho số phức z1; z2. Khi đó tam giác OAB là:
A. Tam giác đều.
B. Tam giác vuông tại O.
C. Tam giác tù.
D. Tam giác có một góc bằng 45o.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Phần thực z1 – 2z2 là – 3, phần ảo của nó là 8.
b) Phần thực và phần ảo của z1.z2 tương ứng là 26 và 7.

Đặt z 1 = x 1 + i y 1 ; z 2 = x 2 + i y 2 .
Từ giả thiết ta có
x 1 2 + y 1 2 = 9 x 2 2 + y 2 2 = 16 x 1 + x 2 2 + y 1 + y 2 2 = 37 ⇒ x 1 x 2 + y 1 y 2 = - 6 x 2 y 1 - x 1 y 2 2 = 108
Vậy z = - 3 8 ± 3 3 8 i
Đáp án A

Chọn B.
Ta có z = z1 – z2 = (2 - 3i) - (4i - 10) = (2 + 10) + (-3 - 4)i = 12 - 7i.

Chọn A.
Ta có: z = z1 + z2 = (-2 + 3i) + (5 + 3i) = (-2 + 5) + (3 + 3)i = 3 + 6i

Chọn B.
Ta có z = z1.z2 = (1 + i) .(1 - 2i) = 1 - 2i + i - 2i2 = 3 - i.
Chọn A.
Ta có ,
,
suy ra:
Lại có
nên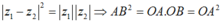
Suy ra AB = OA= OB
Do đó. Tam giác OAB là tam giác đều.