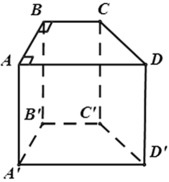
Cho hình lăng trụ đứng ABCD.A'B'C'D' có đáy ABCD là hình thang vuông A ^ = D ^ = 90 0 . Có bao nhiêu cạnh song song với mặt phẳng ( BCC'B' )
A. 3
B. 4
C. 5
D. 6
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
26 tháng 2 2017
Vì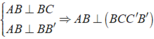
Tương tự: A'B' ⊥ ( BCC'B' ) ⇒ AB,A'B' ⊥ ( BCC'B' )
Chọn đáp án A.
CM
19 tháng 7 2017
Ta có
C ' C ⊥ A B C D , B D ⊥ O C ⇒ B D ⊥ O C ' ⇒ C O C ' ^ = 45 o
∆ O C C ' vuông cân tại C ⇒ C C ' = O C = a 2 2
Vậy V = a 2 . a 2 2 = a 3 2 2
Đáp án D
CM
7 tháng 9 2018
a) Các cạnh song song với cạnh AD là EH, BC, FG.
b) Các cạnh song song với cạnh AB là EF.
c) Các đường thẳng song song với mặt phẳng (EFGH) là: AD, BC, AB, CD.
d) Các đường thẳng song song với mặt phẳng (DCGH): AE, BF.
CM
24 tháng 10 2017
a) Các cạnh song song với cạnh AD là EH, BC, FG.
b) Các cạnh song song với cạnh AB là EF.
c) Các đường thẳng song song với mặt phẳng (EFGH) là: AD, BC, AB, CD.
d) Các đường thẳng song song với mặt phẳng (DCGH): AE, BF.
CM
13 tháng 2 2019
Đáp án A
Từ giả thiết ta có hình thang ABCD là hình thang nội tiếp được đường tròn nên nó là hình thang cân AB = AD = BC = a
Khi đó tâm đường tròn ngoại tiếp hình thang ABCD là trung điểm I của CD và bán kính là r = a.
Ta có:
=> A'A = a 3 . 3 = 3a => V = 3π a 3
Vì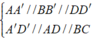
nên các đường thẳng AA',DD',AD,A'D' song song với mặt phẳng ( BCC'B' ).
Chọn đáp án B.