Rút gọn phân thức B = x|x − 2| x 3 − 5x 2 + 6x ta được?
A. B = 1 x − 3 k h i x ≥ 2 ; x ≠ 3
B. B = 1 3 − x k h i x < 2 ; x ≠ 0
C. B = 1 x - 3
D. Cả A, B đều đúng
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

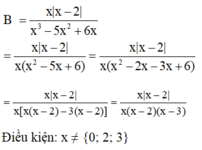
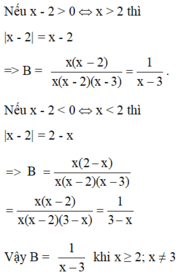
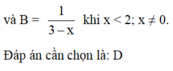

a) (6x+1)2 + (6x-1)2 - 2(1+6x)(6x-1)
= (6x+1+6x-1)2
=144x2
b) x(2x2 -3) - x2(5x+1) +x2
=2x3 - 3x - 5x3 -x2+x2
=-3x3-3x
=-3x(x2+1)
c) 3(22+1)(24+1)(28+1)(216+1)
= (22-1)(22+1)(24+1)(28+1)(216+1)
= (24-1)(24+1)(28+1)(216+1)
= (28-1)(28+1)(216+1)
= (216-1)(216+1)
= 232 -1
d) 3x(x-2) - 5x(1-x) - 8(x2 -3)
= 3x2-6x - 5x + 5x2 - 8x2 +24
= -11x +24

a) \(\left(6x+1\right)^2+\left(6x-1\right)^2-2\left(1+6x\right)\left(6x-1\right)\)
\(=36x^2+12x+1+36x^2-12x+1-72x^2+2\)
\(=4\)
c) \(x\left(2x^2-3\right)-x^2\left(5x+1\right)+x^2\)
\(=2x^3-3x-5x^3-x^2+x^2\)
\(=-3x^3-3x\)
d) \(3x\left(x-2\right)-5x\left(1-x\right)-8\left(x^2-3\right)\)
\(=3x^2-6x-5x+5x^2-8x^2+24\)
\(=-11x+24\)

a) -ĐKXĐ của A:
x+3≠0 ⇔x≠-3.
x2-9≠0 ⇔(x-3)(x+3)≠0 ⇔x-3≠0 hay x+3≠0⇔x≠3 hay x≠-3.
x-3≠0 ⇔x≠3.
b) B=x2+5x+6=x2+2x+3x+6=x(x+2)+3(x+2)=(x+2)(x+3)
c) A=\(\dfrac{x}{x+3}-\dfrac{6x}{x^2-9}+\dfrac{2}{x-3}\)=\(\dfrac{x\left(x-3\right)+2\left(x+3\right)-6x}{\left(x+3\right)\left(x-3\right)}\)=\(\dfrac{x^2-3x+2x+6-6x}{\left(x+3\right)\left(x-3\right)}\)=\(\dfrac{x^2-7x+6}{x^2-9}\)
d)- Vì x=37 thỏa mãn ĐKXĐ của A và A=\(\dfrac{x^2-7x+6}{x^2-9}\)nên:
A=\(\dfrac{37^2-7.37+6}{37^2-9}=\dfrac{279}{340}\)

a: \(=\dfrac{4x\left(3x+1\right)}{\left(3x+1\right)\left(3x-1\right)}=\dfrac{4x}{3x-1}\)
b: \(=\dfrac{2\left(4x^2-4x+1\right)}{4x-30+2x}=\dfrac{4\left(2x-1\right)^2}{6x-30}=\dfrac{2\left(2x-1\right)^2}{3\left(x-5\right)}\)
d: \(=\dfrac{x\left(x-6\right)}{2\left(x-6\right)\left(x+6\right)}=\dfrac{x}{2x+12}\)

b: \(=\dfrac{4x\left(x-1\right)\left(x+1\right)}{6x\left(x-1\right)}=\dfrac{2\left(x+1\right)}{3}\)
c: \(=\dfrac{\left(5-x-1\right)\left(5+x+1\right)}{\left(x+6\right)^2}=\dfrac{\left(4-x\right)\left(x+6\right)}{\left(x+6\right)^2}=\dfrac{4-x}{x+6}\)
d: \(=\dfrac{\left(x+2\right)\left(x+3\right)}{\left(x+2\right)^2}=\dfrac{x+3}{x+2}\)