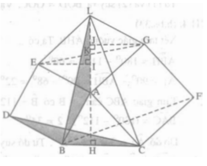
Dựng các hình vuông ABDE và ACFG bên ngoài tam giác nhọn ABC cho trước. Chứng minh rằng các đường thẳng AH, BF, CD đồng quy.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
9 tháng 9 2019
Xét tam giác ALB và ∆BCD có:
AL = BC ( chứng minh b)
AB = BD ( vì ABDE là hình vuông)
∠(BAL) = 90º + ∠(EAL) = 90 + ∠(ABC) = ∠(DBC) .
Suy ra: ∆ALB = ∆BCD ( c.g.c)
Suy ra ∠(ALB) = ∠(BCD) .
Mặt khác ta có ∠(ALB) + ∠(LBH) = 90º nên ∠(BCD) + ∠(LBH) = 90º.
Suy ra LB ⊥ CD, tức CD là một đường cao của tam giác LBC.
7 tháng 3 2020
chán cộng tác viên thế.đọc kĩ vào,x+y=20 chứ ko phải là x-y=20 nhaaaaaaaaa.
Lập luận tương tự câu c), ta có BF là một đường cao của tam giác LBC.
Vậy ba đường thẳng AH, BF, CD là ba đường cao của tam giác LBC nên chúng đồng quy.