Có bao nhiêu cách xếp chỗ ngồi cho 10 bạn, trong đó có An và Bình, và 10 ghế kê thành hàng ngang, sao cho:
a) Hai bạn An và Bình ngồi cạnh nhau?
b) Hai bạn An và Bình không ngồi cạnh nhau?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
19 tháng 11 2019
Đầu tiên ta chỉ dung 7 ghế và xếp An, Chi và 5 bạn không thuộc nhóm An, Chi vào 7 ghế. Ta có 7! cách xếp. Sau đó xếp Bình ngồi cạnh An. Có 2! cách. Cuối cùng xếp Chi, Hương ngồi cùng nhóm với Dung. Ta có 3! cách. Theo quy tắc nhân, có 7! 2! 3! = 60480 cách.
CM
12 tháng 7 2017
a. đầu tiên, xếp chỗ cho An và Bình ngồi cạnh nhau, có 2*8=16 cách. Sau đó, xếp 7 bạn vào 7 chỗ còn lại, nên có 7! Cách xếp. vậy có tất cả 16.7! cách xếp 9 bạn để An và Bình ngồi cạnh nhau.
Chọn D
CM
2 tháng 2 2017
b. Số cách xếp 9 bạn vào 9 chỗ là 9! Cách. Vậy số cách xếp để An và Bình không ngồi cạnh nhau là 9! – 16.7!= 282240
Chọn C
CM
15 tháng 7 2019
a) Xếp 6 nam vào 6 ghế cạnh nhau. Có 6! cách.
Giữa các bạn nam có 5 khoảng trống cùng hai đầu dãy, nên có 7 chỗ có thể đặt ghế cho nữ.
Bây giờ chọn 4 trong 7 vị trí để đặt ghế. Có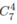 
cách.
Xếp nữ vào 4 ghế đó. Có 4! cách.
Vậy có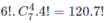 
cách xếp mà không có hai bạn nữ nào ngồi cạnh nhau.
b) Xếp 6 ghế quanh bàn tròn rồi xếp nam vào ngồi. Có 5! cách.
Giữa hai nam có khoảng trống. Xếp 4 nữ vào 4 trong 6 khoảng trống đó. Có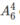 
cách.
Theo quy tắc nhân, có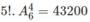 
cách.
CM
15 tháng 1 2019
Chọn A
Số phần tử của không gian mẫu: n ( Ω ) = 5!
Gọi A:”Hai bạn An và Bình không ngồi cạnh nhau”
Thì A ¯ :”Hai bạn An và Bình ngồi cạnh nhau”
Xếp An và Bình ngồi cạnh nhau coi như 1 phần tử
- Xếp 1 phần tử (An+Bình) và 3 bạn còn lại theo các thứ tự khác nhau có: 4! Cách
- Xếp 2 học sinh An và Bình ngồi cạnh nhau có 2! cách
Suy ra 
CM
9 tháng 2 2017
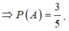
Chọn đáp án A
Phương pháp
Sử dụng nguyên lí vách ngăn.
Cách giải
n(Ω)=5!=120
Xếp Cường, Dũng, Đông vào 3 ghế bất kì có 3! cách, khi đó tạo ra 4 khoảng trống. Xếp An và Bình vào hai trong 4 khoảng trống đó có 4.3 = 12 cách.
Gọi A là biến cố: “An và Bình không ngồi cạnh nhau
a) Có 2. 9 = 18 cách xếp chỗ cho An và Bình ngồi cạnh nhau.
8 bạn kia được xếp vào 8 chỗ còn lại. Vậy có 8! cách xếp 8 bạn còn lại và do đó có 18! 8 cách xếp sao cho An, Bình ngồi cạnh nhau.
b) Có 10! cách xếp chỗ ngồi cho 10 bạn.
Từ đó có 10! - 18. 8! = 72. 8! cách xếp chỗ cho 10 bạn mà An và Bình không ngồi cạnh nhau.