Cho điểm O và đoạn thẳng AB (h.75)
- Vẽ điểm A’ đối xứng với A qua O.
- Vẽ điểm B’ đối xứng với B qua O.
- Lấy điểm C thuộc đoạn thẳng AB, vẽ điểm C’ đối xứng với C qua O.
- Dùng thước để kiểm nghiệm rằng điểm C’ thuộc đoạn thẳng A’B’.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

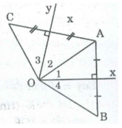
Vì OB = OC nên để điểm B đối xứng với C qua tâm O cần thêm điều kiện B, O, C thằng hàng
∆ OAB cân tại O có Ox là đường trung trực của AB nên Ox cũng là đường phân giác của ∠ (AOB) ⇒ ∠ O 1 = ∠ O 4 (3)
ΔOAC cân tại O có Oy là đường trung trực của AC nên Oy cũng là đường phân giác của ∠ (AOC) ⇒ ∠ O 2 = ∠ O 3 (4)
Vì B, O, C thẳng hàng nên:
∠ O 1 + ∠ O 2 + ∠ O 3 + ∠ O 4 = 180 0 (5)
Từ (3),(4) ; (5) ⇒ 2 ∠ O 1 + 2 ∠ O 2 = 180 0
⇒ ∠ O 1 + ∠ O 2 = 90 0 ⇒ ∠ (xOy) = 90 0
Vậy ∠ (xOy) = 90 0 thì B đối xứng với C qua O

a: Xét (O) có
ΔAMB nội tiếp
AB là đường kính
Do đó: ΔAMB vuông tại M

a: góc AMB=1/2*sđ cung AB=90 độ
góc BMD+góc BCD=180 độ
=>BMDC nội tiếp
b: Xét ΔAMB vuông tại M và ΔACD vuông tại C có
góc MAB chung
=>ΔAMB đồng dạng với ΔACD
=>AM/AC=AB/AD
=>AM*AD=AB*AC=6R^2
c: góc ADC=90-30=60 độ

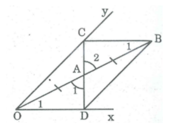
Xét ∆ OAD và ∆ BAC, ta có:
OA = AB (tính chất đối xứng tâm)
∠ A 1 = ∠ A 2 (đối đỉnh)
∠ O 1 = ∠ B 1 (so le trong)
Do đó: ∆ OAD = ∆ BAC (g.c.g)
⇒ AD = AC
Suy ra: C đối xứng với D qua A.
Điểm C’ thuộc đoạn thẳng A’B’