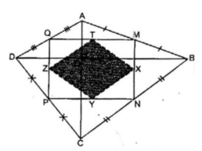
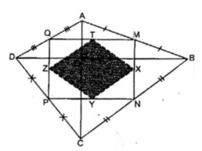
Cho tứ giác ABCD có P và Q là trung điểm của AB và CD, M và N là trung điểm của các đường chéo AC và BD. AC và BD cắt nhau tại H.
Chứng minh rằng:
a) Nếu MN vuông góc với PQ thì BC và AD bằng nhau.
b)Nếu bốn tam giác AHB, BHC, CHD và DHA có diện tích bằng nhau thì ABCD là hình bình hành.