Cho hai đường thẳng chéo nhau ∆ và ∆ ′ có AA’ là đoạn vuông góc chung, trong đó A ∈ ∆ và A′ ∈ ∆ ′. Gọi ( α ) là mặt phẳng chứa AA’ và vuông góc với ∆ ′ và cho biết AA’ = a. Một đường thẳng thay đổi luôn luôn song song với mặt phẳng ( α ) lần lượt cắt ∆ và ∆ ′ tại M và M’ . Hình chiếu vuông góc của M trên mặt phẳng ( α ) là M 1 . Chứng minh rằng khi x thay đổi mặt cầu tâm O luôn luôn chứa một đường tròn cố định.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

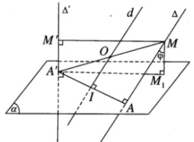
Theo giả thiết ta có: ∠A′M′M = ∠A′AM = ∠A′M1M = 90o
Do đó 5 điểm A, A’, M, M’, M1 cùng thuộc mặt cầu (S) tâm O, với O là trung điểm của A’M và có bán kính r = A′M2
Mặt khác ta có A’M2 = A’A2 + AM2
Trong đó
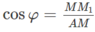
Do đó
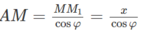
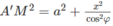
Mặt cầu tâm O có bán kính
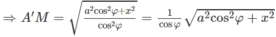
Diện tích của mặt cầu tâm O là:
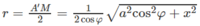

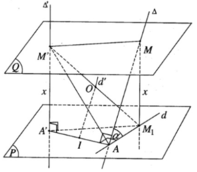
Vì mặt phẳng (P) qua A và vuông góc với Δ′ nên AA’ thuộc (P). Vì M thuộc ∆ mà d là hình chiếu vuông góc của ∆ trên (P) nên M 1 thuộc d. Vì MA ⊥ AA′ ⇒ M 1 A ⊥ AA′
Mặt khác M 1 A ⊥ M′A′ nên ta suy ra M 1 A ⊥ (AA′M′). Do đó M 1 A ⊥ M′A và điểm A thuộc mặt cầu đường kính M’ M 1
Ta có M′A′ ⊥ (P) nên M′A′ ⊥ A′ M 1 , ta suy ra điểm A’ cũng thuộc mặt cầu đường kính M’ M 1
Ta có (Q) // (P) nên ta suy ra
M M 1 ⊥ (Q) mà MM’ thuộc (Q), do đó M 1 M ⊥ MM′
Như vậy 5 điểm A, A’, M, M’, M 1 cùng thuộc mặt cầu (S) có đường kính M’ M 1 . Tâm O của mặt cầu (S) là trung điểm của đoạn M’ M 1
Ta có M ' M 1 2 = M ' A ' 2 + A ' M 1 2 = M ' A ' 2 + A ' A 2 + AM 1 2 = x 2 + a 2 + x 2 cot 2 α vì M M 1 = x
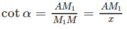
Bán kính r của mặt cầu (S) bằng (M′ M 1 )/2 nên
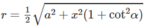

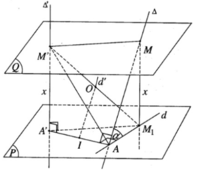
Hình tứ giác A’M’M M 1 là hình chữ nhật nên tâm O cũng là trung điểm của A’M. Do đó khi x thay đổi thì mặt phẳng (Q) thay đổi và điểm O luôn luôn thuộc đường thẳng d’ đi qua trung điểm I của đoạn AA’ và song song với đường thẳng ∆ . Vì mặt cầu tâm O luôn luôn đi qua hai điểm cố định A, A’nên nó có tâm O di động trên đường thẳng d’. Do đó mặt cầu tâm O luôn luôn chứa đường tròn tâm I cố định có đường kính AA’ cố định và nằm trong mặt phẳng cố định vuông góc với đường thẳng d’.

a) Sai
Sửa lại: "Đường thẳng Δ là đường thẳng vuông góc chung của hai đường thẳng chéo nhau a và b nếu Δ cắt cả a và b, đồng thời Δ ⊥ a và Δ ⊥ b"
b) Đúng
c) Đúng
d) Sai
Sửa lại: Đường thẳng đi qua M trên a và vuông góc với a, đồng thời cắt b tại N và vuông góc với b thì đó là đường vuông góc chung của a và b.
e) Sai.


Mặt phẳng
α
chứa A và trục Oy nên có một VTPT là ![]()
Đường thẳng
∆
là giao tuyến của
α
và
β
nên có VTCP ![]()
Theo giả thiết, ta có
u
∆
→
cùng phương với ![]()
Suy ra 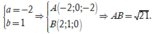
Chọn C.

Câu a) đúng. Khoảng cách của hai đường thẳng chéo nhau là đoạn ngắn nhất trong các đoạn thẳng nối hai điểm bất kì nằm trên hai đường thẳng ấy và ngược lại (xem mục c). Tính chất của khoảng cách giữa hai đường thẳng chéo nhau (Bài 5 – chương III).
Câu b) sai. Qua một điểm có vô số mặt phẳng vuông góc với một mặt phẳng cho trước.
Câu c) sai. Vì trong trường hợp đường thẳng vuông góc với mặt phẳng thì ta có vô số mặt phẳng vuông góc với mặt phẳng cho trước vì bất kì mặt phẳng nào chứa đường thẳng cũng đều vuông góc với mặt phẳng cho trước. Để có khẳng định đúng ta phải nói: Qua một đường thẳng không vuông góc với một mặt phẳng có duy nhất một mặt phẳng vuông góc với mặt phẳng đã cho.
Câu d) sai. Vì đường vuông góc chung của hai đường thẳng phải cắt cả hai đường ấy.

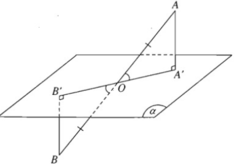
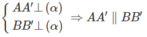
Mặt phẳng (AA', BB') xác định bởi hai đường thẳng song song (AA', BB') cắt mặt phẳng (α) theo giao tuyến qua O, A', B'. Do đó ba điểm O, A', B' thẳng hàng.
Hai tam giác vuông OAA'và OBB' bằng nhau vì có một cạnh huyền và một góc nhọn bằng nhau nên từ đó ta suy ra AA' = BB'.

Câu a) đúng. Khoảng cách của hai đường thẳng chéo nhau là đoạn ngắn nhất trong các đoạn thẳng nối hai điểm bất kì nằm trên hai đường thẳng ấy và ngược lại (xem mục c). Tính chất của khoảng cách giữa hai đường thẳng chéo nhau (Bài 5 – chương III).
Câu b) sai. Qua một điểm có duy nhất một mặt phẳng vuông góc với một mặt phẳng cho trước.
Câu c) sai. Vì trong trường hợp đường thẳng vuông góc với mặt phẳng thì ta có vô số mặt phẳng vuông góc với mặt phẳng cho trước vì bất kì mặt phẳng nào chứa đường thẳng cũng đều vuông góc với mặt phẳng cho trước. Để có khẳng định đúng ta phải nói: Qua một đường thẳng không vuông góc với một mặt phẳng có duy nhất một mặt phẳng vuông góc với mặt phẳng đã cho.
Câu d) sai. Vì đường vuông góc chung của hai đường thẳng phải cắt cả hai đường ấy.
Gọi I là trung điểm của đoạn AA’. Ta có IO // Δ nên tâm O di động trên đường thẳng d cố định đi qua I và song song với ∆ . Mặt cầu tâm O đi qua hai điểm cố định A, A’ , có tâm di động trên đường trung trực d cố định của đoạn AA’. Vậy mặt cầu tâm O luôn luôn chứa đường tròn cố định tâm I có đường kính AA’ nằm trong mặt phẳng AA’ và vuông góc với d.