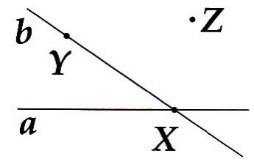
Vẽ hai đường thẳng a, b và ba điểm X, Y, Z đồng thời thỏa mãn những điều kiện sau:
i) X ∈ a, X ∈ b) ii) Y ∈ b, Y ∉ a.) iii) Z ∉ a, Z ∉ b.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
12 tháng 6 2019
Đúng(0)
Những câu hỏi liên quan
ST
1
23 tháng 9 2019
ta có: xy+x+y = 3
=> xy +x +y +1 =4
=> (x+1).(y+1) = 4 (1)
tương tự, ta có: (y+1).(z+1)= 9 (2)
(x+1).(z+1) = 16 (3)
Nhân (1);(2);(3) lại vs nhau
được: \([\left(x+1\right).\left(y+1\right).\left(z+1\right)]^2=576=24^2=\left(-24\right)^2.\)
TH1: (x+1).(y+1).(z+1) = 24
=> 4.(z+1)=24
=> z+1 = 6 => z = 5
mà yz +y +z = 8
=> 6y + 5 = 8 => y = 1/2
mà xz+z+x = 15
=> 6x + 5 = 15 => x = 5/3
=> P = 5/3 +1/2 + 5 = 43/6
TH2: (x+1).(y+1).(z+1) = -24
...
bn cũng lm tương tự như TH1 nha!
14 tháng 11 2018
a, Ta có \(\frac{1}{a}-\frac{1}{b}=\frac{1}{a-b}\)
(=) \(\frac{b}{ab}-\frac{a}{ab}=\frac{1}{a-b}\)
(=) \(\frac{b-a}{ab}=\frac{1}{a-b}\)
(=) \(\left(b-a\right).\left(a-b\right)=ab\)
Vì a,b là 2 số dương
=> \(\hept{\begin{cases}ab>0\left(1\right)\\\left(b-a\right).\left(a-b\right)< 0\left(2\right)\end{cases}}\)
Từ (1) và (2) => Không tồn tại hai số a,b để \(\frac{1}{a}-\frac{1}{b}=\frac{1}{a-b}\)
14 tháng 11 2018
b, Cộng vế với vế của 3 đẳng thức ta có :
\(x+y+y+z+x+z=-\frac{7}{6}+\frac{1}{4}+\frac{1}{12}\)
(=) \(2.\left(x+y+z\right)=-\frac{5}{6}\)
(=) \(x+y+z=\frac{-5}{12}\)
Ta có : \(x+y+z=\frac{-5}{12}\left(=\right)-\frac{7}{6}+z=-\frac{5}{12}\left(=\right)z=\frac{3}{4}\)
Lại có \(x+y+z=\frac{-5}{12}\left(=\right)x+\frac{1}{4}=-\frac{5}{12}\left(=\right)x=-\frac{2}{3}\)
Lại có \(x+y+z=-\frac{5}{12}\left(=\right)y+\frac{1}{12}=-\frac{5}{12}\left(=\right)y=\frac{-1}{2}\)
CM
5 tháng 4 2019
Đường thẳng x là đường thẳng số (2). Đường thẳng y là đường thẳng số (1). Đường thẳng z là đường thẳng số (3)
MT
1
