Cho bốn điểm M, N, P, Q trong đó không có ba điểm nào thẳng hàng. Tìm điểm I sao cho ba điểm M, N, I thẳng hàng và bađiểm P,Q, I thẳng hàng.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
21 tháng 9 2017
bài 1:Qua điểm A và mỗi điểm B,C,D có ba đường thằng là AB, AC,AD. Qua điểm B và mỗi điểm C,D có hai đường thẳng là BC,BD (Không qua A). Qua điểm C và D còn lại có một đường thẳng CD (không đi qua A,B).
Chú ý: có thể trình bày ngắn gọn như sau : với 4 điểm A,B,C,D thì có 6 đường thẳng AB,AC,AD,BC,BD,CD
bài 2:Vì 3 điểm M,N,P thẳng hàng nên đường thẳng đi qua cả 3 điểm M,N,P trùng nhau và Q nằm ngoài đường thẳng trên nên kẻ được 3 đường thẳng lần lượt đi qua 3 điểm thẳng hàng.
Vậy ta có 4 đường thẳng: MP,QN,QM,QP(không kể MN, NP)
CM
11 tháng 9 2018
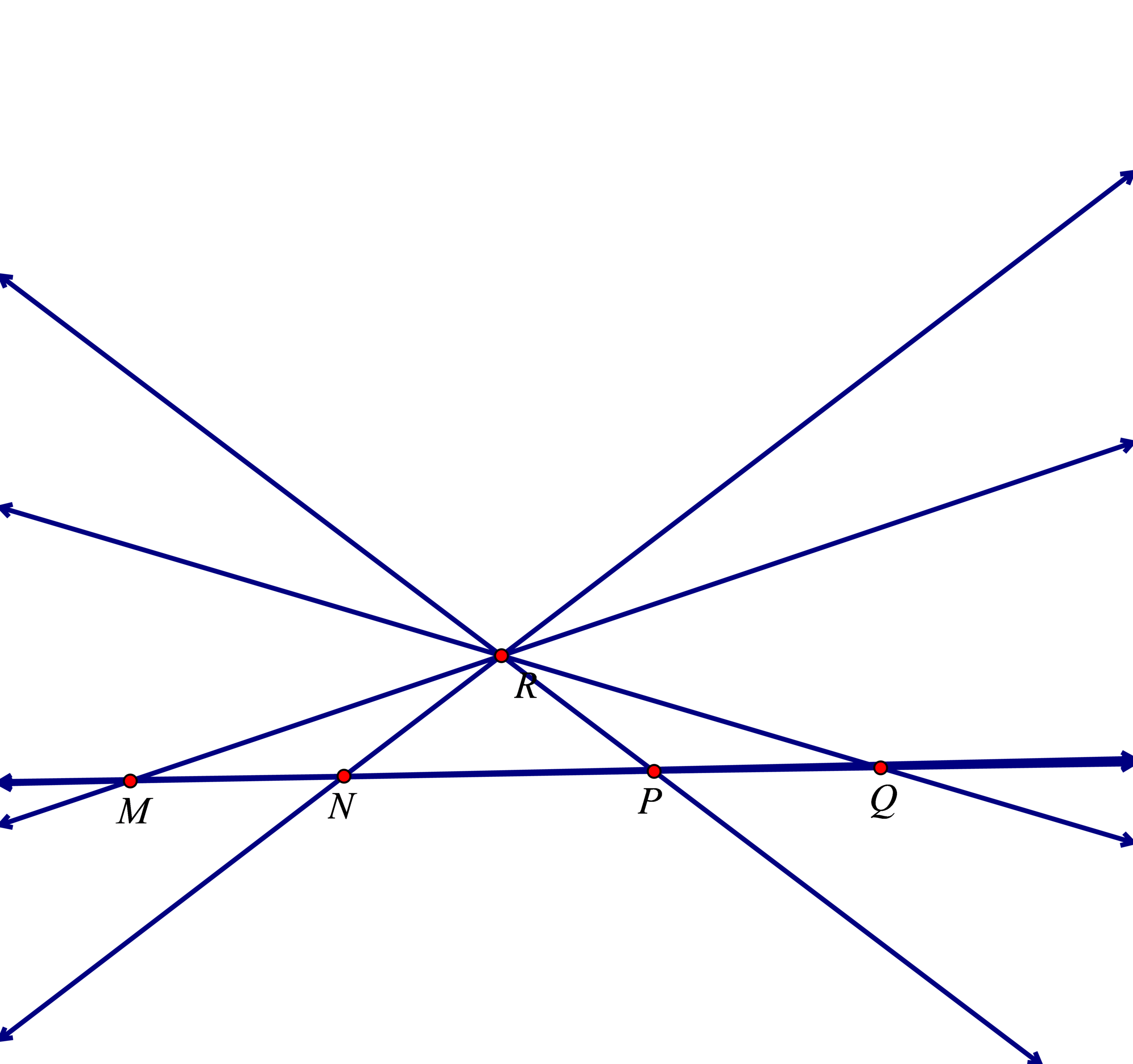
a) Có 5 đường thẳng, đó là đường thẳng MQ, RM, RN, RP, RQ.
b) Các tia gốc P là: PM, PN, PQ, PR. Hai tia PM, PN trùng nhau. Hai tia PM, PQ đối nhau.
29 tháng 11 2021
Giao điểm của AB và CD chính là điểm M thỏa mãn đề bài.
Một lẽ dĩ nhiên là nếu AB song song với CD thì ta không thể tìm được giao điểm của chúng, dẫn đến không tìm được điểm M theo yêu cầu.
CM
3 tháng 1 2017
Bốn điểm G, H, I, K có thẳng hàng vì cả bốn điểm thuộc đường thẳng HI
Điểm I thuộc đường thẳng MN và đường thẳng PQ. Do đó, I là giao điểm của hai đường thẳng MN và PQ.