Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Khi ω = ω 1 mạch xảy ra cộng hưởng, chuẩn hóa R = 1 Z L = Z = 1
Khi ω = 2 ω 1 thì
P = 4 U 2 R cos 2 φ = 2 5 U 2 R ⇒ cos φ = 1 10
c o s φ = 1 10 = 1 1 + 2 X − X 2 2 ⇒ X = 2
Khi ω = 3 ω 1 thì hệ số công suất của mạch sẽ là:
c o s φ = 1 1 + 3 X − X 3 2 = 3 265
Đáp án B
Đáp án C
Chú ý E tỉ lệ thuận với n. Chuẩn hóa R = 1. Áp dụng công thức tính 
Đáp án D
Theo đề ta có:
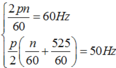
vòng/s
Vậy số cực từ của máy thứ hai là:
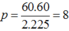cực từ
STUDY TIP
Công thức tính tần số của máy phát điện xoay chiều có p cặp cực từ và roto quay với tốc độ n vòng/s là:
f = p n ( H z )
Lưu ý khi đề không cho chuẩn đơn vị thì chúng ta phải đổi rồi sau đó mới thực hiện tính toán tránh có nhầm lẫn đáng tiếc xảy ra.
Công suất của mạch ngoài \(P = I^2 R = \frac{E^2}{R^2+(Z_L-Z_C)^2}R\)
Mà suất điện động hiệu dụng \(E = \omega\Phi \)
TH1: \(\omega = \omega_0; P_{max}\)
\(P = I^2 R = \frac{E^2}{R^2+(Z_L-Z_C)^2}R\)
\( = \frac{\omega^2 \Phi ^2}{R^2+(Z_L-Z_C)^2}R \)
\( = \frac{ \Phi ^2}{\frac{R^2}{\omega^2}+\frac{Z_L^2}{\omega^2}-2\frac{Z_LZ_C}{\omega^2}+\frac{Z_C^2}{\omega^2}}R \)
\( = \frac{ \Phi ^2}{\frac{1}{\omega^4C^2}+\frac{R^2-2L/C}{\omega^2}+L^2}R \)
\(P_{max} \Leftrightarrow A = (\frac{1}{\omega^4C^2}+\frac{R^2-2L/C}{\omega^2}+L^2)_{min}\)
đặt \(x = \frac{1}{\omega^2}\)
=> \(A_{min} \Leftrightarrow x = \frac{-b}{2a} = \frac{2L/C-R^2}{2/C^2}.\)
=> \(\frac{2}{C^2\omega_0^2} = \frac{2L}{C}-R^2\) hay \(2Z_C^2 = 2Z_LZ_C - R^2 => R^2 =2Z_LZ_C- 2Z_C^2.(1)\)
Ta có \(\frac{P_1}{P_0} = \frac{I_1^2}{I_0^2} = \frac{E_1^2Z_0^2}{E_0^2Z_1^2} = \frac{\omega_1^2Z_0^2}{\omega_0^2Z_1^2} = \frac{4\omega_0^2Z_0^2}{\omega_0^2Z_1^2} = \frac{1}{2}\)
=> \(Z_1^2 = 8Z_0^2\)
=> \(R^2 +(2Z_L - \frac{Z_C}{2})^2 = 8 (R^2 + (Z_L-Z_C)^2) (2)\)
Thay (1) vào (2) ta được \(4Z_L^2 -\frac{7Z_C^2}{4} = 8(Z_L^2 - Z_C^2)\)
=> \(\frac{25}{4}Z_C^2 = 4Z_L^2\) hay \(Z_L = \frac{5}{4}Z_C .(3)\)
Tiếp theo ta xét tỷ số \(\frac{P_2}{P_0} = \frac{\omega_2^2 Z_0^2}{\omega_0^2Z_2^2} = \frac{9.(R^2+(Z_L-Z_C)^2)}{R^2+(3Z_L-Z_C/3)^2}=\frac{9(Z_L^2 - Z_C^2)}{9Z_L^2 - 17/9Z_C^2} = \frac{9(25/4-1)}{9.25/4 - 17/9} = \frac{81/16}{1753/144} = \frac{729}{1753}.\)
=> \(P_2 = \frac{729}{1753}P_0\)
Đáp án thu được như của bạn rồi nhé.
Đáp án B
Nếu quay đồng bộ thì khi đó không có sự chuyển động tương đối giữa roto và cảm ứng từ suy ra không có sự biên thiên từ thông qua khung dây của roto ⇒ trong roto không xuất hiện dòng điện cảm ứng ⇒ không có lực từ ⇒ không có momen làm roto quay ⇒ roto phải quay chậm hơn từ trường quay
⇒ tốc độ góc của động cơ không thể là ω
Đáp án B
Nếu quay đồng bộ thì khi đó không có sự chuyển động tương đối giữa roto và cảm ứng từ , không có sự biên thiên từ thông qua khung dây của roto, trong roto không xuất hiện dòng điện cảm ứng , không có lực từ , không có momen làm roto quay roto phải quay chậm hơn từ trường quay tốc độ góc của động cơ không thể là 6ω...
Đáp án C
Phương pháp: Công thức tính tần số: f = np (n (vòng/s) là tốc độ quay của roto; p là số cặp cực)
Cách giải: Ta có:
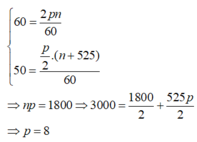
=> Số cực từ của máy thứ 2 là: p/2 = 4
Đáp án: D