Chứng minh rằng: Nếu a + b b + c = c + d d + a (c + d ≠ 0) thì a = c hoặc a = b + c + d = 0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
26 tháng 4 2019
Đúng(0)
Những câu hỏi liên quan
1H
1
19 tháng 2 2021
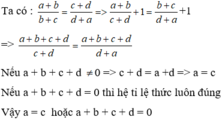
từ a+b/b+c=c+d/d+a=>ad+a^2+bd+ab=bc+bd+c^2+cd
=>ad+ab+a^2-bc-cd-c^2=0
=>ad-cd+ab-bc+a^2-c^2=0
=>(a-c)d+(a-c)b+(a-c)(a+c)=0
=>(a-c)(a+b+c+d)=0
=>a-c=0 hoặc a+b+c+d=0
=>a=c hoặc a+b+c+d=0 (đpcm)
NT
0
L
1
TD
14 tháng 7 2016
\(\left(a+b\right)\left(d+a\right)=\left(c+d\right)\left(b+c\right)\)
\(ad+a^2+bd+ab=bc+bd+c^2+cd\)
\(a\left(b+d\right)+a^2=c\left(b+d\right)+c^2\)
\(a+a^2=c+c^2\)
\(a=c\)
7 tháng 3 2020
Ta có:\(\frac{a+b}{b+c}=\frac{c+d}{d+a}\)
\(\implies\)\(\frac{a+b}{c+d}=\frac{b+c}{d+a}\)
\(\implies\) \(\frac{a+b}{c+d}+1=\frac{b+c}{d+a}+1\)
\(\implies\) \(\frac{a+b+c+d}{c+d}=\frac{a+b+c+d}{d+a}\)
\(\implies\) \(\frac{a+b+c+d}{c+d}-\frac{a+b+c+d}{d+a}=0\)
\(\implies\) \(\left(a+b+c+d\right)\left(\frac{1}{c+d}-\frac{1}{d+a}\right)=0\)
\(\implies\)\(\orbr{\begin{cases}a+b+c+d=0\\\frac{1}{c+d}-\frac{1}{d+a}=0\end{cases}}\)
\(\implies\) \(\orbr{\begin{cases}a+b+c+d=0\\\frac{1}{c+d}=\frac{1}{d+a}\end{cases}}\)
\(\implies\) \(\orbr{\begin{cases}a+b+c+d=0\\c+d=d+a\end{cases}}\)
\(\implies\) \(\orbr{\begin{cases}a+b+c+d=0\\c=a\end{cases}}\)
I
7 tháng 3 2020
ta có \(\frac{a+b}{b+c}=\frac{c+d}{d+a}\)
=>\(\left(a+b\right)\left(a+d\right)=\left(c+d\right)\left(b+c\right)\)
=> \(a^2+ab+ad+bd=c^2+bc+bd+cd\)
=>\(a^2+ab+ad-bc-c^2-cd=0\)
=>\(\left(a^2-c^2\right)+\left(ab-cd\right)+\left(ab-ac\right)=0\)
=>\(\left(a-c\right)\left(a+c\right)+d\left(a-c\right)+b\left(a-c\right)=0\)
=>\(\left(a-c\right)\left(a+b+c+d\right)=0\)
=>\(\orbr{\begin{cases}a-c=0\\a+b+c+d=0\end{cases}\left(dpcm\right)}\)
hacker 2k6
DT
Chứng minh rằng : nếu a+b/b+c=c+d/c+a(c+d khác 0) thì a=c hoặc a+b+c+d=0
giải hộ mik nha
mik cần gấp
3
16 tháng 3 2020
Áp dụng tính chất dãy tỉ số bằng nhau ta có
\(\frac{a+b}{b+c}=\frac{c+d}{c+a}=\frac{a+b+c+d}{a+b+c+d}\)
\(\Rightarrow\orbr{\begin{cases}a+b+c+d=0\\a=c\end{cases}}\)
16 tháng 3 2020
Sửa đề:
Ta có: \(\frac{a+b}{b+c}=\frac{c+d}{d+a}\)
\(\Rightarrow\frac{a+b}{c+d}=\frac{c+b}{d+a}\)
\(\Rightarrow\frac{a+b}{c+d}+1=\frac{c+b}{d+a}+1\)
\(\Rightarrow\frac{a+b+c+d}{c+d}=\frac{c+d+b+d+c}{d+a}\)
Áp dụng t/c dãy tỉ số bằng nhau ta có:
\(\frac{a+b+c+d}{c+d}=\frac{c+d+b+a}{d+a}=\frac{\left(a+b+c+d\right)-\left(c+d+b+c\right)}{\left(c+d\right)-\left(d+a\right)}=\frac{0}{\left(c+d\right)-\left(d+a\right)}=0\)
\(\Rightarrow\frac{a+b+c+d}{c+d}=0\)
Vì \(c+d\ne0\)
\(\Rightarrow a+b+c+d=0\left(đpcm\right)\)
và \(\frac{a+b+c+d}{c+d}-\frac{c+d+b+a}{d+a}=0\)
vd Thay a + b+ c= 1
ta có: \(\frac{1}{c+d}-\frac{1}{d+a}=0\)
\(\Rightarrow\frac{1}{c+d}=\frac{1}{d+a}\)
\(\Rightarrow d+a=c+d\)
\(\Rightarrow a=c\left(đpcm\right)\)
hok tốt!!
24 tháng 8 2021
Ta có: \(\left(a+b+c+d\right)\left(a-b-c+d\right)=\left(a-b+c-d\right)\left(a+b-c-d\right)\)
\(\Leftrightarrow\left(a+d\right)^2-\left(b+c\right)^2=\left(a-d\right)^2-\left(b-c\right)^2\)
\(\Leftrightarrow\left(a+d-a+d\right)\left(a+d+a-d\right)=\left(b+c-b+c\right)\left(b+c+b-c\right)\)
\(\Leftrightarrow2d\cdot2a=2c\cdot2b\)
\(\Leftrightarrow ad=bc\)
hay \(\dfrac{a}{c}=\dfrac{b}{d}\)
TD
2
27 tháng 8 2015
Ta có : \(\frac{a}{b}0\) \(\left(1\right)\)
vì \(ad\)\(
