Trong một khu hội trợ người ta bơm một quả bóng có thể tích 200 lít ở nhiệt độ 270C trên mặt đất. Sau đó bóng được thả bay lên đến độ cao mà ở đó áp suất khí quyển chỉ còn 0,8 lần áp suất khí quyển ở mặt đất và có nhiệt độ 170C. Tính thể tích của quả bóng ở độ cao đó bỏ qua áp suất phụ gây ra bởi vỏ bóng.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
13 tháng 2 2019
Xét quá trình biến đổi của lượng không khí được bơm vào quả bóng
TH1 { v 1 = 125.40 = 5000 c m 3 = 5 l p 1 = p 0 = 10 5 N / m 2
TH2 { v 2 = 2 , 5 l p 2 = ?
p 1 v 1 = p 2 v 2 ⇒ p 2 = p 1 v 1 v 2 = 10 5 .5 2 , 5 = 2.10 5 N / m 2
VT
3 tháng 5 2017
Xét quá trình biến đổi của lượng không khí được bơm vào quả bóng
2 tháng 3 2022
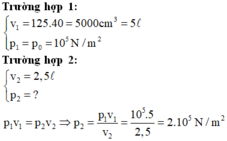
Gọi số quả bóng bay bơm được là \(n\left(quả\right)\)
Trạng thái đầu:
\(\left\{{}\begin{matrix}V_1=50l\\p_1=5MPa=5\cdot10^6Pa\\T_1=37^oC=310K\end{matrix}\right.\)
Trạng thái sau:
\(\left\{{}\begin{matrix}V_2=10n+50\left(l\right)\\p_2=1,05\cdot10^5Pa\\T_2=12^oC=285K\end{matrix}\right.\)
Phương trình trạng thái khí lí tưởng: \(\dfrac{p_1\cdot V_1}{T_1}=\dfrac{p_2\cdot V_2}{T_2}\)
\(\Rightarrow\dfrac{5\cdot10^6\cdot50}{310}=\dfrac{\left(10n+50\right)\cdot1,05\cdot10^5}{285}\)
\(\Rightarrow n=213quả\)
VT
23 tháng 1 2018
Đáp án: C
Ta có:
Thể tích khí bơm được sau 20 lần bơm là 20.0,125 lít
+ Thể tích của không khí trước khi bơm vào bóng: V 1 = 20.0,125 + 2,5 = 5 l (Bao gồm thể tích khí của 20 lần bơm và thể tích khí của khí có sẵn trong bóng)
+ Sau khi bơm khí vào trong bóng thể tích lượng khí chính bằng thể tích của bóng: V 2 = 2,5 l
Do nhiệt đọ không đổi, theo định luật Bôi lơ – Ma ri ốt, ta có:
p 1 V 1 = p 2 V 2 ⇔ 10 5 .5 = p 2 .2,5 ⇒ p 2 = 2.10 5 P a
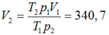
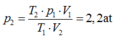
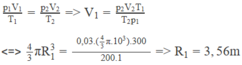
Ta có
Trạng thái 1 { V 1 = 200 l p 1 T 1 = 27 + 273 = 300 K Trạng thái 2 { V 2 = ? p 2 = 0 , 8 p 1 T 2 = 273 + 17 = 290 K
Áp dụng
p 1 V 1 T 1 p 2 V 2 T 2 ⇒ V 2 = p 1 V 1 T 2 p 2 T 1 = p 1 .200.290 0 , 5 p 1 .300 V 2 = 241 , 67 ( l )