Một máy bay đang bay ngang với tốc độ 150 m/s ở độ cao 490 m thì thả một gói hàng. Lấy g = 9,8 m/ s 2 . Tầm bay xa (tính theo phương ngang) của gói hàng là bao nhiêu ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
2 tháng 12 2021
Qũy đạo bay của gói hàng: \(y=\dfrac{g}{2v_0^2}x^2\)
Thời gian rơi: \(t=\sqrt{\dfrac{2h}{g}}=\sqrt{\dfrac{2\cdot490}{10}}=7\sqrt{2}s\)
Tầm bay xa: \(L=v_0t=180\cdot7\sqrt{2}=1781,91m\)
Vận tốc: \(v=\sqrt{\left(gt\right)^2+v_0^2}=\sqrt{\left(10\cdot7\sqrt{2}\right)^2+180^2}=10\sqrt{422}\)m/s
PL
14 tháng 12 2021
Vì khi thả gói hàng, cả máy bay cả hàng đang có vận tốc nên gói hàng sẽ chuyển động theo quán tính => Gói hàng chuyển động ném ngang.
a) Thời gian để gói hàng rơi xuống đất là: 
b) Gọi v0 là tốc độ của gói hàng khi rời khỏi máy bay.
Tầm bay xa của gói hàng là: Lmax = v0t = 150.10 = 1500 m.
c. Quỹ đạo là một phần của parabol.
18 tháng 11 2019
2)v0=150m/s
h =490m
g=9,8m/s2
L=?
GIẢI :
Thời gian rơi của gói hàng :
\(t=\sqrt{\frac{2.490}{9,8}}=10\left(s\right)\)
Tầm xa của gói hàng là:
\(L=v_0t=150.10=1500\left(m\right)\)
18 tháng 11 2019
1) h =80m, v=50m/s; v0 =?
GIẢI :
Lấy g =10m/s2
Thời gian rơi là :
\(t=\sqrt{\frac{2h}{g}}=\sqrt{\frac{2.80}{10}}=4\left(s\right)\)
Ta có công thức : \(v=\sqrt{v_0^2+\left(gt\right)^2}=\sqrt{v_0^2+\left(10.4\right)^2}\)
=> \(50=\sqrt{v_0^2+\left(10.4\right)^2}\)
=> \(v_0=30m/s\)
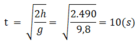
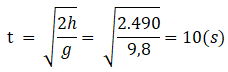
Gọi v 0 là tốc độ của gói hàng khi rời khỏi máy bay. Ta có:
L m a x = v 0 t = 150.10 = 1500 m.