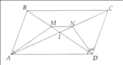
Cho hình bình hành ABCD. Phân giác của  v à D ^ cắt các đường chéo BD và AC lần lượt tại M và N. Chứng minh: MN song song với AD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

CM
Cao Minh Tâm
11 tháng 8 2018

Đúng(0)
Những câu hỏi liên quan

5 tháng 2 2020
Gọi \(I\) là giao điểm điểm \(BD\)và \(AC\).
Xét \(\Delta ABD\)có tia p.giác \(AM\)có: \(\frac{AB}{AD}=\frac{BM}{DM}\)
Tương tự ta có: \(\frac{CD}{AD}=\frac{CN}{AN}\)
Mà: \(AB=CD\Rightarrow\frac{BM}{DM}=\frac{CN}{AN}\)
Từ trên ta suy ra: \(\frac{BM}{DM}+1=\frac{CN}{AN}+1\Leftrightarrow\frac{BD}{DM}=\frac{AC}{AN}\Leftrightarrow\frac{AI}{DM}=\frac{AI}{AN}\)
\(\Rightarrow MN//AD\left(đpcm\right)\)