Cho tam giác ABC có BC = 15cm, AC = 18cm, AB = 12cm. Gọi I và G lần lượt là tâm đường tròn nội tiếp và trọng tâm tam giác ABC.
a) Chứng minh IG song song với BC.
b) Tính độ dài đoạn thẳng IG.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
5 tháng 10 2019
Đúng(0)
Những câu hỏi liên quan
CM
26 tháng 12 2019
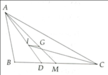
Do M là trung điểm BC nên MB = 1 2 BC = 1 2 .15 = 7,5 cm
Mà BD = 6cm nên DM = 7,5 cm – 6cm = 1,5 cm
Do IG // DM nên I G D M = A G A M = 2 3 => IG = 2 3 DM = 1 3 .1,5 = 1 cm
Đáp án: A
29 tháng 7 2017
1/. _Kẻ pg AD và đ/cao AE (D ; E thuộc BC) ta thấy AG/AE=2/3_bt:(1)
Trong tg ABC vớí pg AD ta có : DB/DC= AB/AC=6/12=1/2 <=> BD=3 ; DC=6 (cm)
Trong tg ABD với pg BI ta có : IA/IB=AB/BD =3/6 <=>AI/AD=2/3 -bt:(2). từ (1) & (2)suy ra đpcm
góc AED=^ACB=48 độ ( hai góc đều cọng với góc^BED thì =180 độ
KN
13 tháng 7 2020
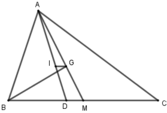
a) Gọi D, E, F lần lượt là chân các đường phân giác của tam giác ABC lần lượt hạ từ A, B, C.
Gọi T là trung điểm của BC. Do AD là đường phân giác của tam giác ABC nên \(\frac{BD}{AB}=\frac{CD}{AC}\Rightarrow\frac{BD}{5}=\frac{CD}{7}=\frac{BD+CD}{5+7}=\frac{6}{12}=\frac{1}{2}\)\(\Rightarrow\hept{\begin{cases}BD=2,5\\CD=3,5\end{cases}}\)
\(\Delta ABD\) có BI là đường phân giác nên \(\frac{AI}{ID}=\frac{BA}{BD}=\frac{5}{2,5}=2\)
Do G là trọng tâm của tam giác ABC nên \(\frac{AG}{GT}=2\)
Từ các kết quả trên ta được \(\frac{AI}{ID}=\frac{AG}{GT}=2\)suy ra IG // DT hay IG // BC (Theo định lý Thales đảo)
b) Ta có \(\Delta BMI=\Delta BDI\)vì \(BD=BM=2,5;\widehat{DBI}=\widehat{MBI}\); BI là cạnh chung
Suy ra \(\widehat{BMI}=\widehat{BDI}\)
Chứng minh tương tự \(\Delta CNI=\Delta CDI\Rightarrow\widehat{ CNI}=\widehat{CDI}\)
Mà \(\widehat{BDI}+\widehat{CDI}=180^0\)nên \(\widehat{BMI}+\widehat{CNI}=180^0\)suy ra\(\widehat{AMI}+\widehat{ANI}=180^0\)
Vậy tứ giác AMIN nội tiếp hay bốn điểm A, M, I, N cùng nằm trên 1 đường tròn (đpcm)
22 tháng 2 2018
Cách làm của bạn trên sai rồi nhưng đáp số đúng làm lại cho tự vẽ hình lấy :))
Gọi D là tiếp điểm của đường tròn (I) với AB. Ta tính được BC = 15 ( cm )
\(AD=\frac{AB+AC-BC}{2}=\frac{9+12-15}{2}=3\left(cm\right)\)
Gọi N là giao điểm của BI và AC. Ta có:
\(\frac{BI}{BN}=\frac{BD}{BA}=\frac{6}{9}=\frac{2}{3}=\frac{BM}{BG}\Rightarrow\)IG // NM và \(IG=\frac{2}{3}NM\)
Lần lượt tính AN = 4,5 ( cm ) ; AM = 6 ( cm )
Suy ra NM = 1,5 ( cm ) nên IG = 1( cm )
Vậy IG = 1 ( cm )
21 tháng 2 2018
Gọi J,D thứ tự là trung điểm BC,BA.
Hạ: GE', IE 
BA.
JD là đường trung bình 
ABC nên: JD = 1/2AC = 6
JA = 1/2BC = 15/2
AD = 1/2AB = 9/2
AG/AJ = AE'/AD = 2/3 => AE' = 3
Lại có: AE = AC + AB - BC/2 = 3 => E \(\equiv\) E' => G; I; E
=> IG = EG' - IE' = 1 (cm)
*P/s: Sai đâu thì bn sửa nhé*
