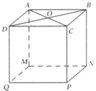
Cho hình hộp chữ nhật ABCD.MNPQ có tất cả các cạnh bằng nhau. Gọi o là giao điểm của AC và BD.
a) Tứ giác ABNM là hình gì? Vì sao?
b) Cho SCDQP = 100 cm2. Tính OB
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
31 tháng 5 2018
Đúng(0)
Những câu hỏi liên quan
18 tháng 1 2022
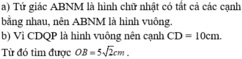
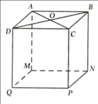
a: Xét tứ giác ABNM có
AM//BN
AM=BN
Do đó: ABNM là hình bình hành
mà \(\widehat{MAB}=90^0\)
nên ABNM là hình chữ nhật
mà AM=AB
nên ABNM là hình vuông
b: Xét ΔMBC có
MN là đường trung tuyến
MN=BC/2
Do đó: ΔMBC vuông tại M
Xét tứ giác MDCN có
MD//CN
MD=CN
Do đó: MDCN là hình bình hành
mà MD=DC
nên MDCN là hình vuông
Xét tứ giác MPNQ có
\(\widehat{MPN}=\widehat{MQN}=\widehat{PMQ}=90^0\)
Do đó: MPNQ là hình chữ nhật
5 tháng 1 2022
a: xét tứ giác ADFE có
AE//DF
AE=DF
Do đó: ADFE là hình bình hành
mà \(\widehat{EAD}=90^0\)
nên ADFE là hình chữ nhật
mà AE=AD
nên ADFE là hình vuông
c: Xét tứ giác BEDF có
BE//DF
BE=DF
Do đó: BEDF là hình bình hành
Suy ra: DE//BF và DE=BF(1)
hay ME//NF
Xét tứ giác BEFC có
BE//FC
BE=FC
Do đó: BEFC là hình bình hành
=>EC và BF cắt nhau tại trung điểm của mỗi đường
=>N là trung điểm của BF
=>FN=BF/2(2)
Ta có: AEFD là hình vuông
=>AF và DE vuông góc với nhau tại trung điểm của mỗi đường và bằng nhau
=>M là trung điểm của DE
=>EM=DE/2(3)
Từ (1), (2) và (3) suy ra EM=FN
Xét tứ giác EMFN có
EM//FN
EM=FN
Do đó: EMFN là hình bình hành
mà \(\widehat{EMF}=90^0\)
nên EMFN là hình chữ nhật
CM
29 tháng 5 2019
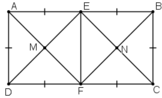
a) E, F là trung điểm AB, CD ⇒ AE = EB = AB/2, DF = FC = CD/2.
Ta có: AB = CD = 2AD = 2BC
⇒ AE = EB = BC = CF = FD = DA.
+ Tứ giác ADFE có AE // DF, AE = DF
⇒ ADFE là hình bình hành.
Hình bình hành ADFE có Â = 90º
⇒ ADFE là hình chữ nhật.
Hình chữ nhật ADFE là hình chữ nhật có AE= AD
⇒ ADFE là hình vuông.
b) Tứ giác DEBF có EB // DF, EB = DF nên là hình bình hành
Do đó DE // BF
Tương tự: AF // EC
Suy ra EMFN là hình bình hành
Theo câu a, ADFE là hình vuông nên ME = MF, ME ⊥ MF.
Hình bình hành EMFN có M̂ = 90º nên là hình chữ nhật.
Lại có ME = MF nên EMFN là hình vuông.
AH
Akai Haruma
Giáo viên
4 tháng 1 2021
Lời giải:a) Vì $ABCD$ là hình chữ nhật nên $AB=CD$
$\Rightarrow \frac{AB}{2}=\frac{CD}{2}$$\Leftrightarrow AE=DF$
$AB\parallel CD\Rightarrow AE\parallel DF$
Như vậy, tứ giác $ADFE$ hai cạnh đối $AE, DF$ song song và bằng nhau nên $ADFE$ là hình bình hành.
Mà $\widehat{D}=90^0$ nên $ADFE$ là hình chữ nhật.
Hình chữ nhật $ADFE$ có 2 cạnh kề $AD=\frac{AB}{2}=AE$ nên $ADFE$ là hình vuông.
b)
Vì $ADFE$ là hình vuông nên $AD\perp AF\Rightarrow \widehat{EMF}=90^0$. Đồng thời, $\widehat{DEF}=45^0$
Tương tự: $EBCF$ cũng là hình vuông $\Rightarrow \widehat{ENF}=90^0; \widehat{FEC}=45^0$
Từ đây suy ra $\widehat{MEN}=\widehat{DEF}+\widehat{FEC}=90^0=\widehat{EMF}=\widehat{ENF}=90^0$ nên tứ giác $EMFN$ là hình chữ nhật.
Mặt khác: Vì $AEDF, BEFC$ là 2 hình vuông bằng nhau (do $AE=EB$) nên đường chéo $ED=EC\Rightarrow EM=EN$
Hình chữ nhật $EMFN$ có 2 cạnh kề $EM=EN$ nên $EMFN$ là hình vuông.
