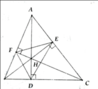
Cho tam giác nhọn ABC có các đường cao AD, BE và CF đồng quy tại H. Chứng minh:
a) Δ A F N ∽ Δ M D C ; ;
b) H là giao điểm các đường phân giác của Δ D EF ;
c) B H . B E + C H . C F = B C 2 .
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
9 tháng 4 2017
Đúng(0)
Những câu hỏi liên quan
25 tháng 2 2023
a: Xét tứ giác BFEC có
góc BFC=góc BEC=90 độ
=>BFEC nội tiếp
=>góc BFE+góc BCE=180 độ
=>góc AFE=góc ACB
mà góc FAE chung
nên ΔAFE đồng dạng với ΔACB
b: Xét tứ giác BFHD có
góc BFH+goc BDH=180 độ
=>BFHD là tứ giác nội tiếp
Xét tứ giác CEHD có
góc CEH+góc CDH=180 độ
=>CEHD là tứ giác nội tiếp
góc FDH=góc FBH
góc EDH=góc ACF
mà góc FBH=góc ACF
nên góc FDH=góc EDH
=>DH là phân giác của góc FDE(1)
góc EFH=góc CAD
góc DFH=góc EBC
mà góc CAD=góc EBC
nên góc EFH=góc DFH
=>FH là phân giác của góc EFD(2)
Từ (1), (2) suy ra H là giao của ba đường phân giác của ΔDEF
c: Xét ΔBHD vuông tại D và ΔBCE vuông tại E có
góc HBD chung
=>ΔBHD đồg dạng với ΔBCE
=>BH/BC=BD/BE
=>BH*BE=BC*BD
Xét ΔCDH vuông tại Dvà ΔCFB vuông tại F có
góc FCB chung
=>ΔCDH đồng dạng với ΔCFB
=>CD/CF=CH/CB
=>CD*CB=CH*CF
=>BH*BE+CH*CF=BC^2
25 tháng 2 2022
a: Xét tứ giác BCEF có
\(\widehat{BFC}=\widehat{BEC}=90^0\)
Do đó:BCEF là tứ giác nội tiếp
b: Xét tứ giác AEHF có
\(\widehat{AEH}+\widehat{AFH}=180^0\)
Do đó: AEHF là tứ giác nội tiếp
NL
4 tháng 5 2021
a) Xét \(\Delta ABE\) và \(\Delta ACF\) có:
\(\widehat{AEB}=\widehat{AFC}\)
\(\widehat{A}\) chung
\(\Rightarrow\Delta ABE\sim\Delta ACF\left(gn\right)\)
b) Vì \(\Delta ABE\sim\Delta ACF\)
\(\Rightarrow\widehat{ABE}=\widehat{ACF}\left(1\right)\)
Theo bài ra, ta có: AB // d
\(\Rightarrow\widehat{ABE}=\widehat{BED}\left(2\right)\)
Từ (1) và (2)
\(\Rightarrow\widehat{ACF}=\widehat{BED}\)
Xét \(\Delta HED\) và \(\Delta HEC\) có:
\(\widehat{BED}=\widehat{ACF}\)
\(\widehat{EHC}\) chung
\(\Rightarrow\Delta HED\sim\Delta HEC\left(g-g\right)\)
\(\Rightarrow\dfrac{HE}{HD}=\dfrac{HC}{HE}\)
\(\Leftrightarrow HE^2=HD.HC\)
11 tháng 5 2023
a: góc AEH+góc AFH=180 độ
=>AEHF nội tiếp
Xét tứ giác BFEC có
góc BFC=góc BEC=90 độ
=>BFEC nội tiếp
=>góc AFE=góc ACB
=>ΔAFE đồng dạng với ΔACB
b: MF/MB=HF/HB
NE/NC=HE/HC
Xét ΔHFE và ΔHBC có
góc HFE=góc HBC
góc FHE=góc BHC
=>ΔHFE đồng dạng với ΔHBC
=>HF/HB=HE/HC
=>MF/MB=NE/NC
