Tìm parabol (P): y = ax2 + 3x – 2 biết rằng có trục đối xứng x = -3. A. y = x2 + 3x – 2. B. 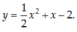C. ...
Đọc tiếp
Tìm parabol (P): y = ax2 + 3x – 2 biết rằng có trục đối xứng x = -3.
A. y = x2 + 3x – 2.
B. 
C. 
D. 
K
Khách
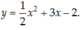
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
24 tháng 6 2021
a) Thay x=1 và y=-2 vào (P), ta được:
\(a\cdot1^2-4\cdot1+c=-2\)
\(\Leftrightarrow a-4+c=-2\)
hay a+c=-2+4=2
Thay x=2 và y=3 vào (P), ta được:
\(a\cdot2^2-4\cdot2+c=3\)
\(\Leftrightarrow4a-8+c=3\)
hay 4a+c=11
Ta có: \(\left\{{}\begin{matrix}a+c=2\\4a+c=11\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-3a=-9\\a+c=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=3\\c=2-a=2-3=-1\end{matrix}\right.\)
Vậy: (P): \(y=3x^2-4x-1\)
CM
14 tháng 5 2017
+ Parabol y = ax2 + bx + 2 có trục đối xứng x = –3/2
⇒ –b/2a = –3/2 ⇒ b = 3a (1)
+ Parabol y = ax2 + bx + 2 đi qua điểm A(3; –4)
⇒ –4 = a.32 + b.3 + 2 ⇒ 9a + 3b = –6 (2).
Thay b = 3a ở (1) vào biểu thức (2) ta được:
9a + 3.3a = –6 ⇒ 18a = –6 ⇒ a = –1/3 ⇒ b = –1.
Vậy parabol cần tìm là y = –1/3x2 – x + 2.
AH
Akai Haruma
Giáo viên
5 tháng 1 2022
Lời giải:
Parabol đi qua $A(2;19)$ nên $y_A=3x_A^2+bx_A+c$ hay $19=12+2b+c$
$\Rightarrow 2b+c=7(1)$
$x=\frac{-2}{3}$ là trục đối xứng
$\Leftrightarrow \frac{-b}{2.3}=\frac{-2}{3}$
$\Rightarrow b=4(2)$
Từ $(1); (2)\Rightarrow c=-1$
Vậy parabol có pt $y=3x^2+4x-1$
5 tháng 1 2022
Theo đề, ta có:
\(\left\{{}\begin{matrix}\dfrac{-b}{6}=\dfrac{-2}{3}\\12+2b+c=19\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=4\\c=-1\end{matrix}\right.\)
CM
1 tháng 3 2019
Vì parabol (P) cắt trục Ox tại điểm có hoành độ bằng 2 nên A(2; 0) thuộc (P).
Thay x = 0; y = 2 vào phương trình parabol ta được 0 = 4a + 6 – 2 hay a = -1
Chọn D.
Vì parabol (P) có trục đối xứng x = -3 nên:
Chọn D.