Tồn tại giá trị của m để hai đường thẳng sau cắt nhau tại một điểm trên trục hoành: (m-1) x+ my-5=0 và mx+ (2m-1)y + 7=0. Khẳng định nào sau đây là đúng?
A. m> 2
B. m< 0
C. 1< m< 2
D. 0<m<1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a.
Để đường thẳng đi qua A
\(\Rightarrow2.1-m^2-m=0\Leftrightarrow m^2+m-2=0\)
\(\Rightarrow\left[{}\begin{matrix}m=1\\m=-2\end{matrix}\right.\)
b.
Hoành độ giao điểm của (d) với trục hoành:
\(2x+4=0\Rightarrow x=-2\Rightarrow\) hai đường thẳng cắt nhau tại (-2;0)
(d') đi qua (-2;0) nên:
\(-2+m-2=0\Rightarrow m=4\)

Để hai đường thẳng d1; d2 cắt nhau tại một điểm nằm trên d3 khi và chỉ khi 3 đường thẳng d1; d2; d3 đồng quy.
Giao điểm của d1 và d3 là nghiệm hệ phương trình:
x − 2 y + 1 = 0 x + y − 5 = 0 ⇔ x = 3 y = 2 ⇒ A ( 3 ; 2 )
Do 3 đường thẳng này đồng quy nên điểm A thuộc d2. Suy ra:
3m - (3m-2).2 + 2m – 2= 0
⇔ 3m – 6m + 4 + 2m – 2 = 0 ⇔ - m + 2 = 0 ⇔ m= 2
Với m= 2 thì đường thẳng d2 : 2x - 4y + 2= 0 hay x- 2y + 1 =0 . Khi đó, đường thẳng d1 và d2 trùng nhau.
Vậy không có giá trị nào của m thỏa mãn.
ĐÁP ÁN D

a/ \(A\left(-2;-4\right);B\left(1;0\right)\)
Gọi pt AB có dạng \(y=ax+b\Rightarrow\left\{{}\begin{matrix}-2a+b=-4\\a+b=0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}a=\frac{4}{3}\\b=-\frac{4}{3}\end{matrix}\right.\) \(\Rightarrow y=\frac{4}{3}x-\frac{4}{3}\)
b/ Để hai đường thẳng cắt trục hoành \(\Rightarrow\left\{{}\begin{matrix}m\ne0\\m\ne1\end{matrix}\right.\)
Hoành độ giao điểm của (d1) và Ox:
\(\left(m-1\right)x-5=0\Rightarrow x=\frac{5}{m-1}\)
Hoành độ giao điểm của (d2) và Ox:
\(mx+7=0\Rightarrow x=-\frac{7}{m}\)
\(\Rightarrow\frac{5}{m-1}=-\frac{7}{m}\Rightarrow m=\frac{7}{12}\)

Bài 1)
a) Xét phương trình hoành độ giao điểm: \(2x+3+m=3x+5-m\)
\(\Leftrightarrow x=3+m+m-5\Leftrightarrow x=2m-2\)
Để giao điểm của hai đường thẳng trên nằm trên trục tung thì \(2m-2=0\Leftrightarrow m=1\)
b) Do (d) // (d') nên (d) có phương trình \(y=-\frac{1}{2}x+b\)
Do (d) cắt trục hoành tại điểm có hoành độ x = 10 nên điểm (10;0) thuộc đường thẳng (d0.
Vậy thì \(0=-\frac{1}{2}.10+b\Leftrightarrow b=5\)
Vậy phương trình đường thẳng (d) là \(y=-\frac{1}{2}x+5\)
Bài 2)
a) Để (d1)//(d2) thì \(4m=3m+1\Leftrightarrow m=1\)
b) Để (d1)//(d2) thì \(4m\ne3m+1\Leftrightarrow m\ne1\)
Khi m = 2, ta có phương trình hoành độ giao điểm là:
\(8x-7=7x-7\Leftrightarrow x=0\)
Với \(x=0,y=-7\)
Vậy tọa độ giao điểm của (d1) và (d2) là (0; -7)
+ Hai đường thẳng cắt nhau tại một điểm trên trục hoành suy ra tung độ giao điểm là y=0.
+ Từ đây ta có: (m-1)x-5=9 suy ra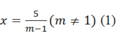
Đồng thời: mx+7=0 suy ra x= -7/m ( m≠0) (2)
+ Từ (1) và (2) ta có:
Chọn D.