Cho tập hợp A={0;1;2;3;4;5}. Có thể lập bao nhiêu số tự nhiên chẵn có 4 chữ số khác nhau?
A. 752
B. 160
C. 156
D. 240
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
28 tháng 11 2019
a, x – 9 = 13 => x = 13 + 9 => x = 22
Vậy M = {22} và M có 1 phần tử
b, x + 6 = 34
x = 34 – 6
x = 28
Vậy H = {28} và H có 1 phần tử.
c, x.0 = 0 luôn đúng với mọi x ∈ N
Vậy O = N và O có vô số phần tử
d, a) x.0 = 3 không thỏa mãn vì trong tập hợp các số tự nhiên, số nào nhân với 0 cũng bằng 0
Vậy A = { ∅ } và A có 0 phần tử
e, (x – 2)(x – 5) = 0
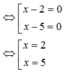
Vậy N = {2;5} và N có 2 phần tử
f, a) x : 0 = 0 không có số tự nhiên nào thỏa mãn vì không thể chia cho 0
Vậy G = { ∅ } và G có 0 phần tử
HD
1 tháng 4 2020
cho tập hợp A = { -3 ;-2 ; 0 ; 6 ; 9 }. trong các 1 tập hợp sau tập hợp nào ko phải là tập hợp con của A ?
A. {-3 , 9} B. {-2 , 0 , -9 } C. {-3 ,0 , 6 ,9 } D . {-2}
15 tháng 9 2021
Tập hợp C rỗng vì \(x^2+7x+12=0\Leftrightarrow x\in\left\{-3;-4\right\}\notin N\)
\(a,\left\{1;2\right\};\left\{1;3\right\};\left\{2;3\right\}\\ b,\left\{1\right\};\left\{2\right\};\left\{3\right\};\left\{1;2\right\};\left\{1;3\right\};\left\{2;3\right\};\left\{1;2;3\right\}\)
\(X=\left\{1;3\right\}\\ X=\left\{1;2;3\right\}\\ X=\left\{1;3;4\right\}\\ X=\left\{1;3;5\right\}\\ X=\left\{1;2;3;4\right\}\\ X=\left\{1;2;3;5\right\}\\ X=\left\{1;3;4;5\right\}\\ X=\left\{1;2;3;4;5\right\}\)
Số tự nhiên thỏa mãn có dạng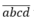
với a,b,c,d ∈ A và đôi một khác nhau.
TH1: d=0
Có 5 cách chọn a; 4 cách chọn b và 3 cách chọn c nên theo quy tắc nhân có 5.4.3 = 60 số.
TH2: d ≠ 0 ; d có 2 cách chọn là 2, 4
Khi đó có 4 cách chọn a( vì a khác 0 và khác d); có 4 cách chọn b và 3 cách chọn c.
Theo quy tắc nhân có: 2.4.4.3=96 số
Vậy có tất cả: 96 + 60 = 156 số.
Chọn C.