Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Nếu chọn một học sinh nam có 280 cách.
Nếu chọn một học sinh nữ có 325 cách.
Theo qui tắc cộng, ta có 280 + 325 = 605 cách chọn.
Chọn đáp án D.
a) Theo quy tắc cộng, nhà trường có 280 + 325 = 605 cách chọn
b) Theo quy tắc nhân, nhà trường có 280.325 = 91000 cách chọn
Chúc bạn học tốt ~
a. Theo quy tắc cộng, nhà trường có : 280+325=605280+325=605 cách chọn.
b. Theo quy tắc nhân, nhà trường có : 280.325=91000280.325=91000 cách chọn.
Chọn B.
Số phần tử của không gian mẫu:
Gọi A là biến cố “nhóm được chọn có cả nam và nữ, đồng thời mỗi khối có 1 học sinh nam”
⇒ số phần tử của biến cố A là: 
.
Không gian mẫu là số cách chọn ngẫu nhiên 3 học sinh từ 13 học sinh.
Suy ra số phần tử của không gian mẫu là 
.
Gọi A là biến cố 3 học sinh được chọn có cả nam và nữ đồng thời có cả khối 11 và khối 12
Ta có các trường hợp thuận lợi cho biến cố A là:
● Trường hợp 1. Chọn 1 học sinh khối 11; 1 học sinh nam khối 12 và 1 học sinh nữ khối 12 nên có 
cách.
● Trường hợp 2. Chọn 1 học sinh khối 11; 2 học sinh nữ khối 12 có 
cách.
● Trường hợp 3. Chọn 2 học sinh khối 11; 1 học sinh nữ khối 12 có 
cách.
Suy ra số phần tử của biến cố A là 
Vậy xác suất cần tính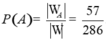 
Chọn D.
a) Theo quy tắc cộng có: 23 +17 = 40 cách chọn một học sinh tham gia cuộc thi môi trường. Vì vậy chọn đáp án C
Nhận xét: học sinh có thể dộc không kĩ đề: chọn 1 học sinh nữ trong 23 học sinh nữ nên có 23 cách chọn (phương án A); hoặc chọn một học sinh nam trong số 17 học sinh nam nên có 17 cách chọn (phương án B); hoặc nhầm sang quy tắc nhân nên có 23 * 17 = 391 cách chọn
Đáp án đúng C
n(omega)=\(C^7_{18}\)
\(n\left(\overline{A}\right)=C^7_{13}+C^7_{11}+C^7_{12}\)
=>\(P\left(A\right)=1-\dfrac{2838}{31824}=\dfrac{4831}{5304}\)
Số cách chọn 7 em bất kì trong ba khối: \(C|^7_{18}=31824\) (cách)
- Số cách chọn 7 em đi trong 1 khối:
\(C^7_7=1\) (cách)
- Số cách chọn 7 em đi trong 2 khối:
+) 7 em trong khối 12 và 11:
\(C^7_{13}-C^7_7=1715\) (cách)
+) 7 em trong khối 12 và 10:
\(C^7_{12}-C^7_7=791\) (cách)
+) 7 em trong khối 11 và 10:
\(C^7_{11}=330\) (cách)
→ Số cách chọn 7 em đi có cả ba khối:
31824 - 1 -1715 - 791 - 330 = 28987(cách)
Đáp án :C
Nhà trường có hai cách chọn:
Trường hợp 1. Chọn 1 học sinh nam. có 307 cách
Trường hợp 2. Chọn 1 học sinh nữ. Có 326 cách
Vậy, có 307 + 326 = 633 cách chọn một học sinh tham dự cuộc thi trên.