Hàm số y = f(x) liên tục trên R và có bảng biến thiên dưới đây. Khẳng định nào sau đây là đúng?
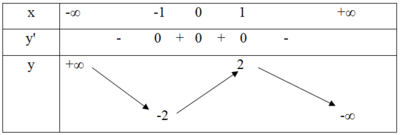
A. Hàm số có ba điểm cực trị
B. Hàm số đạt cực đại tại x = 0
C. Hàm số đạt cực tiểu tại x = -1
D. Hàm số đạt cực đại tại x = 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D.
Từ bảng biến thiên của hàm số ta có hàm số đạt cực đại tại x = 0 , y C D = 5 ; hàm số đạt cực tiểu tại x = 4 , y C T = − 3. Do đó phương án đúng là D.
Phân tích phương án nhiễu.
Phương án A: Sai do HS nhầm với giá trị cực tiểu của hàm số.
Phương án B: Sai do HS nhầm với giá trị cực đại của hàm số.
Phương án C: Sai do HS nhầm với điểm cực tiểu của hàm số.

Đáp án D.
Từ bảng biến thiên của hàm số ta có hàm số đạt cực đại tại x = 0 , y C D = 5 hàm số đạt cực tiểu tại x = 4, y C T = - 3 Do đó phương án đúng là D.

Chọn D
Xét hàm số ![]() .
.
Có ![]()
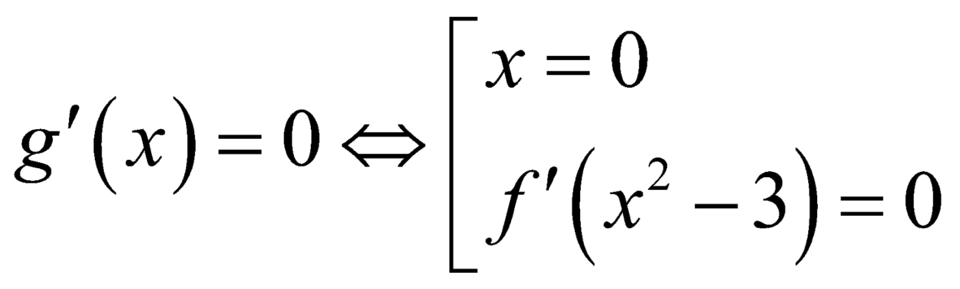
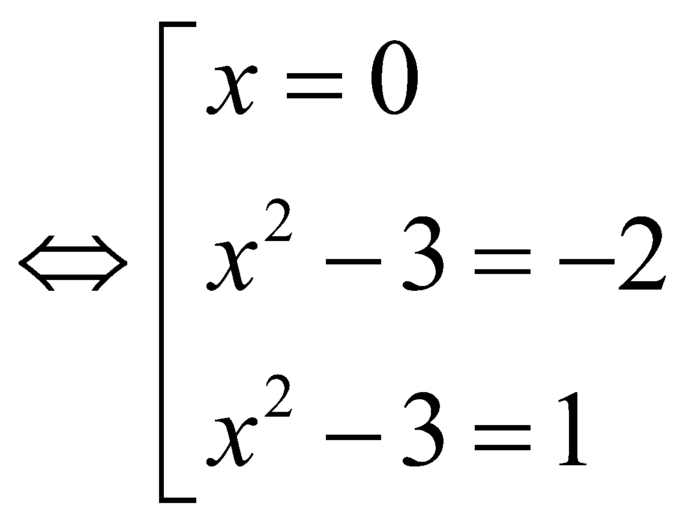
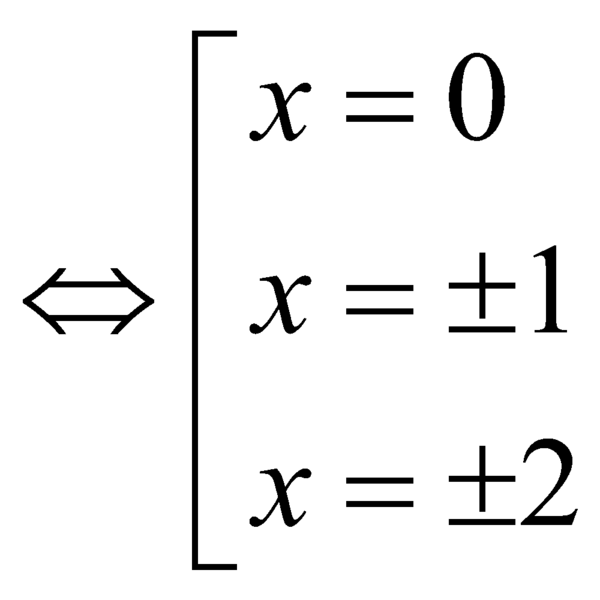 .
.
Ta lại có ![]() thì
thì ![]() . Do đó
. Do đó ![]() thì
thì ![]() .
.
![]() thì
thì ![]() . Do đó
. Do đó ![]() thì
thì ![]() .
.
Từ đó ta có bảng biến thiên của ![]() như sau
như sau
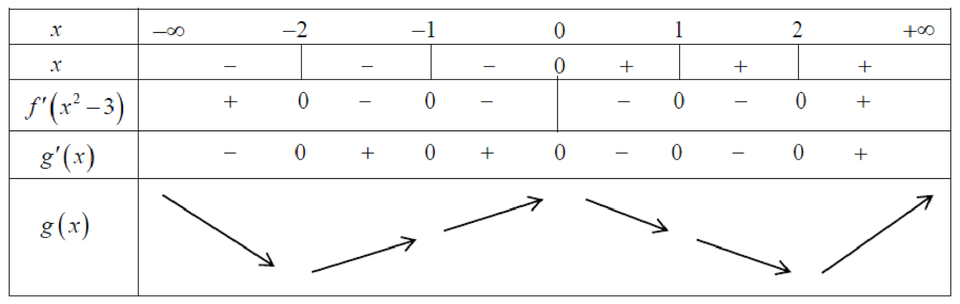
Dựa vào bảng biến thiên, ta có
I. Hàm số ![]() có 3 điểm cực trị . LÀ MỆNH ĐỀ ĐÚNG.
có 3 điểm cực trị . LÀ MỆNH ĐỀ ĐÚNG.
II. Hàm số ![]() đạt cực tiểu tại
đạt cực tiểu tại ![]() LÀ MỆNH ĐỀ SAI.
LÀ MỆNH ĐỀ SAI.
III. Hàm số ![]() đạt cực đại tại
đạt cực đại tại ![]() LÀ MỆNH ĐỀ SAI.
LÀ MỆNH ĐỀ SAI.
IV. Hàm số ![]() đồng biến trên khoảng
đồng biến trên khoảng ![]() LÀ MỆNH ĐỀ ĐÚNG.
LÀ MỆNH ĐỀ ĐÚNG.
V. Hàm số ![]() nghịch biến trên khoảng
nghịch biến trên khoảng ![]() LÀ MỆNH ĐỀ SAI.
LÀ MỆNH ĐỀ SAI.
Vậy có hai mệnh đề đúng.
ở chỗ x<1=> x= -2 thì sao bạn ơi =>(x^2 -3) =1 >0 thì sao f ' (...)>0 được ????

Đáp án A
Hàm số f(x) xác định trên D⊆ R
Điểm
x
0
∈ D được gọi là điểm cực đại của hàm số f(x) nếu tồn tại một khoảng (a;b)⊂ D sao cho
x
0
∈ (a;b) và f(
x
0
)>f(x),∀x ∈ (a,b)∖{
x
0
}.

Đáp án A
Hàm số f(x) xác định trên D⊆ R
Điểm xo∈ D được gọi là điểm cực đại của hàm số f(x) nếu tồn tại một khoảng (a;b)⊂ D sao cho xo∈ (a;b) và f(xo)>f(x),∀x ∈ (a,b)∖{xo}.


Hình ảnh trên là một phần đồ thị của y trên tập xác định. Ta thấy rằng hàm số đạt cực đại tại x = 2 nhưng không chắc rằng có còn điểm cực đại nào khác trên những khoảng rộng hơn hay không (I) sai, (III) đúng.
Hàm số không xác định tại x = 1 nên không thể đạt cực tiểu tại điểm này =>(II) sai.
Chọn B
Đáp án : C.