Hỏi phương trình 3x2- 6x+ ln( x+1) 3+1=0 có bao nhiêu nghiệm phân biệt?
A. 2.
B. 1.
C. 3.
D. 4.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 3 2022
Pt đã cho có 2 nghiệm pb khi:
\(\left\{{}\begin{matrix}m+1\ne0\\\Delta'=\left(m+3\right)^2-\left(m+1\right)\left(2m+9\right)>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne-1\\-m^2-5m>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne-1\\-5< m< 0\end{matrix}\right.\)
\(\Rightarrow m=\left\{-4;-3;-2\right\}\) có 3 giá trị nguyên
CM
23 tháng 8 2018
Đáp án C
Điều kiện: 
.
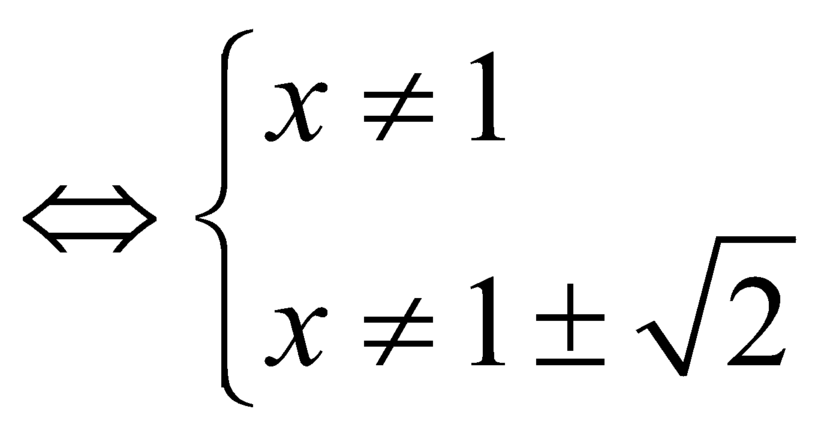Xét hàm số 
có 
; 
.
Chia 
cho 
ta được:
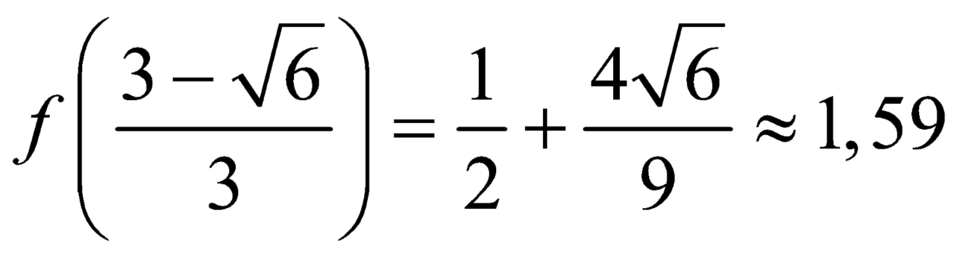
Bảng biến thiên và đồ thị:
Đặt 
.
Phương trình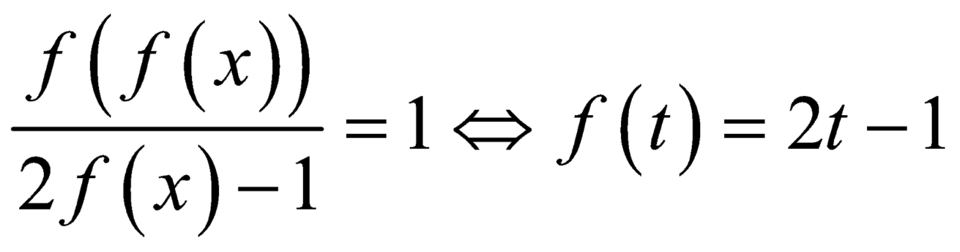 
.
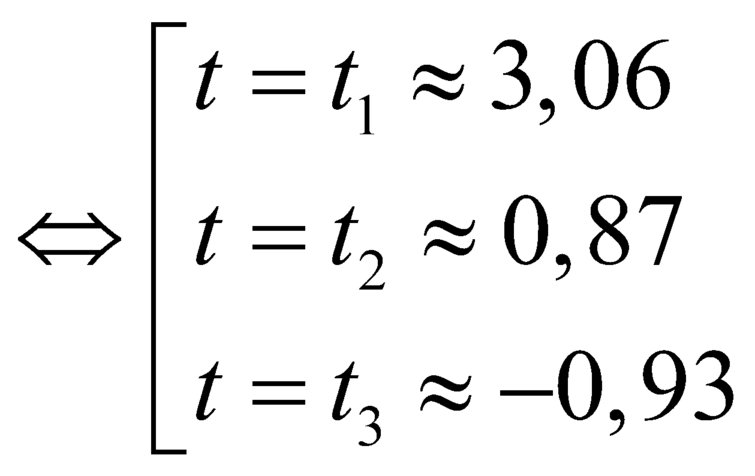
Với 
, từ đồ thị ta thấy phương trình này chỉ cho 1 nghiệm.
Với 
, từ đồ thị ta thấy phương trình này cho 3 nghiệm.
Với 
, từ đồ thị ta thấy phương trình này chỉ cho 1 nghiệm.
Vậy phương trình đã cho có 5 nghiệm phân biệt.
17 tháng 5 2023
a: Khi m=1 thì (1) sẽ là:
x^2-x-8=0
=>\(x=\dfrac{1\pm\sqrt{33}}{2}\)
b: 3x1^2+3x2^2+2x1x2=5
=>3[(x1+x2)^2-2x1x2]+2x1x2=5
=>3[(2m-1)^2-2(-8m)]+2(-8m)=5
=>3(4m^2-4m+1+16m)-16m=5
=>12m^2+36m+3-16m-5=0
=>12m^2+20m-2=0
=>\(m=\dfrac{-5\pm\sqrt{31}}{6}\)
CM
4 tháng 5 2018
Đáp án A
Ghi nhớ: Nếu hàm số 
liên tục trên đoạn 
và 
thì phương trình 
có ít nhất một nghiệm nằm trong khoảng 
.
PT
1
CM
12 tháng 2 2017
Phương trình bậc hai a x 2 + b x + c = 0 có hai nghiệm âm phân biệt khi Δ > 0, (-b)/a < 0, c/a > 0. Ta có
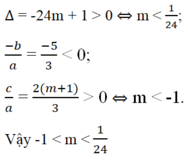
Đáp án: B
Điều kiện: x> -1
Ta có: 3x2- 6x+ ln( x+1) 3+1=0 hay 3x2- 6x+ 3ln( x+1)+1=0
f(x)=3x2- 6x+ 3ln( x+1) +1=0 ⇒ f ' ( x ) = 6 x - 6 + 3 x + 1
Đạo hàm f’ (x) = 0 khi và chỉ khi (2x- 2) (x+ 1) +1=0
⇔ x = ± 1 2
Từ đây, ta có bảng biến thiên của f(x):
Nhìn vào bảng biến thiên ta sẽ có phương trình đã cho có 3 nghiệm phân biệt.
Chọn C.