Cho hình nón có bán kính đáy là 4cm và chiều cao 6cm. Thể tích của một hình cầu bằng thể tích hình nón. Tính bán kính hình cầu?
A. r = 18 3 c m
B. r = 2cm
C. r = 24 3 c m
D. r = 4 3 c m
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Tính được r = 1,44cm Þ Smc = 4p r 2 = 26,03 c m 2
b, Ta có V c = 4 3 πR 2 = 15 , 8 cm 3 => R = 1,56cm
=> V h n = 1 3 πR 2 h ≈ 2 , 53 πcm 3

a) Với giả thiết ở đề bài, ta có thể tính được r từ đó tính được diện tích mặt cầu gần bằng \(26cm^2\)
b) Tương tự câu a, ta tính được thể tích hình nón là \(7,9cm^3\)

Gọi H là tâm mặt đáy của hình nón, O là tâm mặt cầu (S), đường thẳng IH cắt mặt cầu (S) tại điểm K.


Phương pháp:
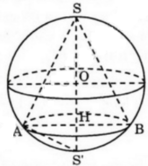
+ Hình nón có chiều cao h và bán kính R thì có thể tích là
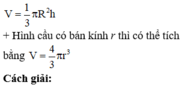
Vì hình nón có bán kính R và chiều cao h bằng nhau nên h = R và thể tích hình nón đã cho là

Khi đó H là tâm đường tròn ngoại tiếp tam giác SAB và H cũng là tâm mặt cầu ngoại tiếp hình nón đỉnh S.
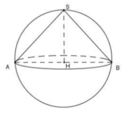
Nên bán kính mặt cầu là HS = R nên thể tích hình cầu này
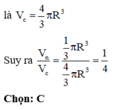

Hình vẽ đâu bn.(không có hình thì mik ko bt AB là đường sinh hay chiều cao nhé. Nhưng thường thì AB là đường sinh)
(nếu đề bài AB là đường cao thì bn đăng lại nhé)
\(Sxq=\pi\left(r+R\right)l=\pi\left(3+6\right)4=36\pi\left(cm^2\right)\)
\(Stp=\pi\left(r+R\right)l+\pi\left(r^2+R^2\right)=36\pi+\pi\left(3^2+6^2\right)=36\pi+45\pi\)
\(=81\pi\left(cm^2\right)\)
có: \(h=\sqrt{l^2-\left(R-r\right)^2}=\sqrt{4^2-\left(6-3\right)^2}=\sqrt{7}cm\)
\(V=\dfrac{1}{3}\pi\left(r^2+R^2+rR\right).h\)\(=\dfrac{1}{3}\pi.\left(3^2+6^2+3.6\right).\sqrt{7}=21\sqrt{7}.\pi\left(cm^3\right)\)

Lời giải:
Diện tích xung quanh hình nón:
$\pi (r+R).l=\pi (6+3).4=36\pi$ (cm vuông)
Diện tích toàn phần:
$36\pi+\pi r^2+\pi R^2=36\pi +\pi.3^2+\pi. 6^2=81\pi$ (cm vuông)
Thể tích:
Chiều cao hình nón: $\sqrt{4^2-(6-3)^2}=\sqrt{7}$ (cm)
$\frac{1}{3}\pi (r^2+R^2+r.R)h=\frac{1}{3}\pi (3^2+6^2+3.6).\sqrt{7}=21\sqrt{7}\pi$ (cm khối)
Đáp án C