Cho tam giác vuông ABC tại A, đường cao AH. Đường tròn đường kính BH cắt AB tại D, đường tròn đường kính CH cắt AC tại E. Chọn khẳng định sai trong các khẳng định sau
A. DE là cát tuyến của đường tròn đường kính BH
B. DE là tiếp tuyến của đường tròn đường kính BH
C. Tứ giác AEHD là hình chữ nhật
D. DE ⊥ DI (với I là trung điểm BH)

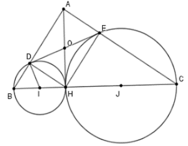
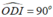

Chọn đáp án A
Gọi I, J lần lượt là trung điểm của BH và CH.
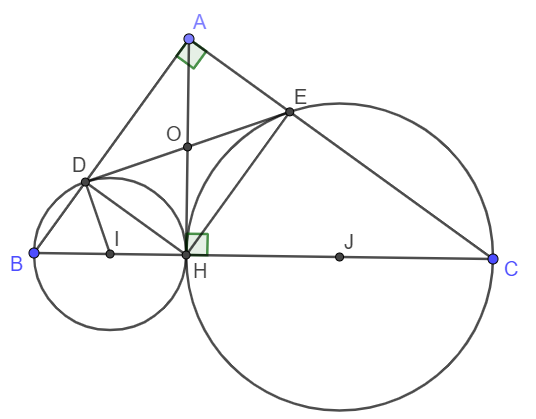
Để chứng minh DE là tiếp tuyến của đường tròn tâm I đường kính BH ta chứng minh ID ⊥ DE hay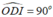
Vì D, E lần lượt thuộc đường tròn đường kính BH và HC
Nên DE là tiếp tuyến của đường tròn đường kính BH
Từ chứng minh trên suy ra các phương án B, C, D đúng