Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
\(BH=\sqrt{10^2-8^2}=6\left(cm\right)\)
\(CH=\dfrac{AH^2}{BH}=\dfrac{8^2}{6}=\dfrac{64}{6}=\dfrac{32}{3}\left(cm\right)\)
Vì tam giác ABC vuông tại A nên
Theo định lý Pytago ta có:
Vậy AC ≈ 4,38 (cm); BC 6,65 (cm)
Đáp án cần chọn là: B
Vì tam giác ABC vuông tại A nên
Theo định lý Py-ta-go ta có:
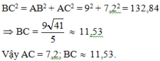
Đáp án cần chọn là: D
a, HB = 1,8cm; CH = 3,2cm; AH = 2,4cm; AC = 4cm
b, AB = 65cm; AC = 156cm; BC = 169cm; BH = 25cm
c, AB = 5cm; BC = 13cm; BH = 25/13cm; CH = 144/13cm
Áp dụng định lý Py - ta - Go vào tam giác ABC vuông tại A có :
AC2 = BC2 - AB2
AC2 =
Ta có :
Mà :
⇒
⇔ AH =
a) Áp dụng pi ta go ta có : AB2 = AH2 + BH2 = 162 + 252 = 881
=> AB =
Lại có : BH.HC = AH2
<=> HC.25 = 162
<=> HC.25 = 256
<=> HC = 256 : 25 = 10,24
Ta có : BC = HC + BH = 10,24 + 25 = 35,24
Áp dụng bi ta go : AC2 = AH2 + HC2 = 162 + 10,242 = 360,8576
=> AC =
Ta có AB : AC = 4 : 5 ⇔ A B 4 = A C 5 ⇒ A B 2 16 = A C 2 25 = A B 2 + A C 2 16 + 25 = 41 41 = 1
(Vì theo định lý Py-ta-go ta có A B 2 + A C 2 = B C 2 ⇔ A B 2 + A C 2 = ( 41 ) 2 = 41 )
Nên A B 2 16 = 1 ⇒ A B 2 = 16 ⇒ AB = 4; A C 2 25 = 1 ⇒ AC = 5
Theo hệ thức lượng trong tam giác vuông ABC ta có:
A C 2 = C H . B C ⇒ C H = A C 2 B C = 25 41 ≈ 3 , 9
Vậy CH ≈ 3,9
Đáp án cần chọn là: D