Cho hình thang vuông ABCD A ^ = D ^ = 90 0 , trong đó có C ^ = 45 0 , AB = 2cm, CD = 4cm. Diện tích của hình thang vuông ABCD là
A. 3 c m 2
B. 8 c m 2
C. 4 c m 2
D. 6 c m 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

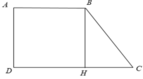
Xét hình thang ABCD
Từ B kẻ BH ⊥ CD, khi đó ta được hình chữ nhật ABHD ⇒ AB = DH = 2cm
⇒ HC = CD - DH = 4 - 2 = 2cm.
+ Xét Δ BDC có BH là đường cao đồng thời là đường trung tuyến
⇒ Δ BDC là tam giác cân tại B.

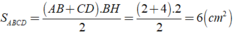
Chọn đáp án D.
Cho hình thang vuông ABCD(góc A = góc D=90 độ),biết AB=2cm,CD=4cm,góc C = 45 độ.Tính diện tích ABCD.


ko bt' vẽ hình
bài giải:
vẽ BH là đường cao của hình thang ABCD
ta có: tam giác BHC cân tại H( vì gCBH=HCB=90o)
do đó HB=HC
SABCD là ( 2+ 4) *2/2=8( cm2)
Tính diện tích hình thang vuông có \(\widehat{A}=\widehat{D}=90^{0^{ }}\) ,AB = 2cm, CD = BC = 5cm ?

Kẻ BH⊥CD thì BH//AD, BH⊥AB
BH//AD và AB//HD nên ABHD là hbh
\(\Rightarrow AB=DH=2\left(cm\right);AD=BH\\ \Rightarrow CH=CD-DH=3\left(cm\right)\)
Pytago: \(AD^2=BH^2=BC^2-DH^2=16\left(cm\right)\)
\(\Rightarrow AD=4\left(cm\right)\\ \Rightarrow S_{ABCD}=\dfrac{1}{2}AD\left(AB+CD\right)=\dfrac{1}{2}\cdot4\cdot7=14\left(cm^2\right)\)

Xét tam giác ABD và tam giác BDC có:
\(\widehat{BAD}=\widehat{DBC}=90^o\)
\(\widehat{ABD}=\widehat{BDC}\) (Cùng phụ với góc \(\widehat{ADC}\) )
\(\Rightarrow\Delta ABD\sim\Delta BDC\left(g-g\right)\Rightarrow\frac{AB}{BD}=\frac{BD}{DC}\Rightarrow BD^2=\frac{AB}{DC}\)
Xét tam giác vuông ABD, áp dụng định lý Pi-ta-go ta có:
\(DB^2=AB^2+AD^2=2^2+4^2=20\)
Suy ra \(2=\frac{20}{DC}\Rightarrow DC=10cm\)
Xét tam giác vuông BDC, áp dụng định lý Pi-ta-go ta có:
\(BC^2=DC^2-BD^2=10^2-20=80\Rightarrow BC=\sqrt{80}\left(cm\right)\)
Vậy chu vi hình thang vuông bằng: 2 + 4 + 10 + \(\sqrt{80}=14+\sqrt{80}\left(cm\right)\)
Diện tích hình thang bằng: \(\frac{\left(2+10\right).4}{2}=24\left(cm^2\right)\)
Xét hình thang ABCD
Từ B kẻ BH ⊥ CD, khi đó ta được hình chữ nhật ABHD ⇒ AB = DH = 2cm
⇒ HC = CD - DH = 4 - 2 = 2cm.
+ Xét Δ BDC có BH là đường cao đồng thời là đường trung tuyến
⇒ Δ BDC là tam giác cân tại B.
Chọn đáp án D.