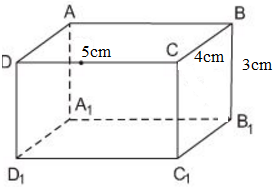
Các kích thước của hình hộp chữ nhật ABCD.A1B1C1D1 là DC = 5cm, CB = 4cm, BB1 = 3cm. Hỏi độ dài DC1 và CB1 là bao nhiêu xentimet?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
26 tháng 4 2018
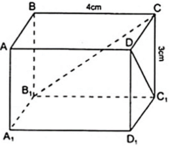
DC1 ∈ mp( DCC1D1 ) với D C C 1 D 1 là hình chữ nhật nên Δ DCC1 vuông tại C.
Áp dụng định lý Py – ta – go vào Δ DCC1 vuông tại C ta được: DC12 = CC12 + CD2
Hay DC12 = 32 + 52 ⇔ DC12 = ( √ (34) )2 ⇔ DC1 = √ (34) ( cm )
CB1 ∈ ( BCC1B1 ) là hình chữ nhật nên Δ BCB1 vuông tại B.
Áp dụng định lí Py – ta – go vào Δ BCB1 vuông tại B ta được: CB12 = CB2 + BB12
Hay CB12 = 32 + 42 = 52 ⇔ CB1 = 5( cm )
Vậy DC1 = √ (34) ( cm ); CB1 = 5( cm )
22 tháng 4 2017
Vì ABCD.A1B1C1D1 là hình hộp chữ nhật nên DCC1D1 và CBB1C1 là hình chữ nhật.
=> CC1 = BB1 = 3cm
CM
12 tháng 12 2017
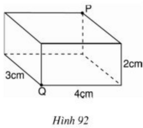
Vì con kiến phải bò theo mặt của hình hộp từ Q đến P tức phải bò trên "một mặt phẳng". Ta vẽ hình khai triển của hình hộp chữ nhật và trải phẳng như sau:
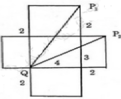
Khi đó, P sẽ có hai vị trí là P1 và P2. Và quãng đường ngắn nhất sẽ là một trong hai đoạn thẳng QP1 hoặc QP2.
14 tháng 6 2019
Chu vi đáy của hình hộp chữ nhật là :
(3+4)×2=14(cm)
Diện tích xung quanh là :
14×5=70(cm)
Thể tích hình hộp chữ nhật là :
3×4×5=60(cm)
Đ/S:....
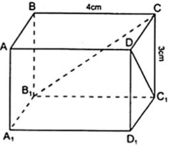
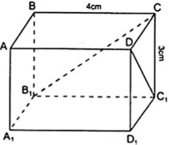
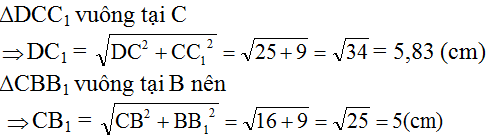
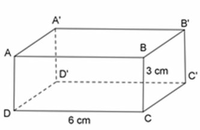
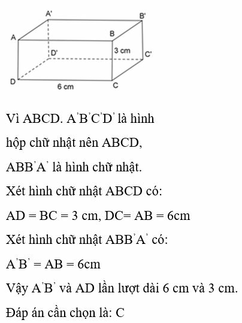
Vì ABCD.A1B1C1D1 là hình hộp chữ nhật
⇒ DCC1D1 và CBB1C1 là hình chữ nhật.
⇒ CC1 = BB1 = 3cm
ΔDCC1 vuông tại C, áp dụng định lí Py-ta–go ta có:
DC12 = DC2 + CC12
ΔCBB1 vuông tại B, áp dụng định lí Py–ta-go ta có:
CB12= CB2 + BB12