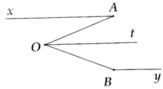
Cho hình vẽ bên, biết O A x ^ = 30°, O B y ^ = 150° và Ot là tia phân giác của A O B ^ = 60°. Chứng minh ba đường thẳng Ax, By và Ot đôi một song song
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
18 tháng 7 2021
Bài 1:
Vì ∠AOC = ∠BOD (đối đỉnh)
Vì ∠AOC + ∠BOD = 140o (gt)
⇒ ∠AOC = ∠BOD = 140o/2 = 70o
Ta có: ∠AOC + ∠AOD = ∠COD (2 góc kề bù)
Thay số: 70o + ∠AOD = 180o
∠AOD = 180o - 70o
∠AOD = 110o
Vì ∠AOD = ∠BOC (đối đỉnh)
⇒ ∠BOC = 110o
Vậy ∠AOC = 70o
∠BOD = 70o
∠AOD = 110o
∠BOC = 110o
CM
28 tháng 7 2017
a) B O D ^ = A O C ^ = 60° (đối đỉnh.).
=> C O B ^ + A O C ^ = 180° (kề bù), => B O C ^ = 180 ° − A O C ^ = 120°
=> A O D ^ = B O C ^ = 120° (đối đỉnh),
b) Vì Ot là phân giác góc AOC nên
A O t ^ = 1 2 A O C ^ = 30°
=> B O t ' ^ = A O t ^ = 30° (đối đỉnh).
Tương tự:
D O t ' ^ = 30 ° ⇒ B O t ' ^ = D O t ' ^
Do đó Ot' là phân giác của B O D ^ .
9 tháng 4 2021
a) Ta có: \(\widehat{xOm}+\widehat{yOm}=180^0\)(Hai góc kề bù)
\(\Leftrightarrow\widehat{yOm}+30^0=180^0\)
hay \(\widehat{yOm}=150^0\)
Vậy: \(\widehat{yOm}=150^0\)
9 tháng 4 2021
b) Ta có: tia Ot là tia phân giác của \(\widehat{xOy}\)
nên \(\widehat{yOt}=\widehat{xOt}=\dfrac{\widehat{xOy}}{2}=\dfrac{180^0}{2}\)
hay \(\widehat{yOt}=90^0\)(đpcm)
22 tháng 9 2021
Ta có: \(\widehat{AOt}=\widehat{BOt}=\dfrac{\widehat{AOB}}{2}=60^0:2=30^0\)(do Ot là phân giác \(\widehat{AOB}\))
Ta có: \(\widehat{AOt}=\widehat{OAx}=30^0\)
Mà 2 góc này so le trong
=> Ax//Ot(1)
Ta có: \(\widehat{BOt}+\widehat{OBy}=30^0+150^0=180^0\)
Mà 2 góc này là 2 góc trong cùng phía
=> By//Ot(2)
Từ (1),(2) => đpcm
Vì Ot là phân giác A O B ^ nên:
= A O t ^ = B O t ^ = 1 2 A O B ^ = 1 2 . 60° = 30°
=> x A O ^ = A O t ^ => Ax // Ot (1)
Lại có : t O A ^ + O B y ^ = 30° +150° = 180° => Ot // By. (2)
Từ (1) và (2), ta có Ax // By // Ot