Cho hình chóp đều S.ABCD có cạnh đáy bằng 4 cm và cạnh bên bằng 3 c m . Cắt hình chóp bởi mặt phẳng (P) song song với mặt phẳng đáy và cách đáy một khoảng 2 cm.
a) Tính chiều cao của hình chóp đều phần chứa đỉnh S sau khi cắt hình chóp đều S.ABCD bởi (P).
b) Tính diện tích một mặt bên hình chóp cụt đều

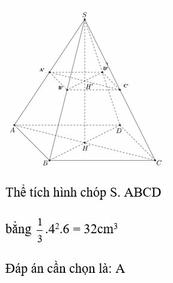
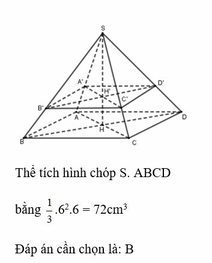



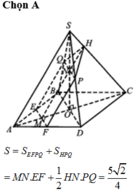
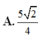
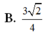
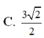
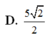
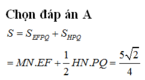
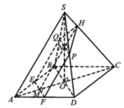
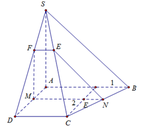

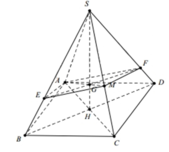
a) Gọi O là tâm của đáy ABCD, M là giao điểm của SO và mặt phẳng (P). Ta có: OM = 2(cm).
Ta tính được O B = 2 2 c m rồi suy ra SO = 5 (cm)
Từ đó chiều cao cần tìm là: SM = SO - OM 3 (cm)
b) Gọi I là trung điểm của BC. E, F, J lần lượt là giao điểm của SB, SC, SI với mặt phẳng (p).