Biết rằng hàm số y = a x 2 + bx + c (a ≠ 0) đạt giá trị lớn nhất bằng 3 tại x = 2 và có đồ thị hàm số đi qua điểm A (0; −1). Tính tổng S = a + b + c.
A. S = -1
B. S = 4
C. S = - 4
D. S = 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Từ giả thiết, ta có hệ:
− b 2 a = − 2 4 a − 2 b + c = 5 a + b + c = − 1 ⇔ a = − 2 3 ; b = − 8 3 ; c = 7 3
⇒ S = a 2 + b 2 + c 2 = 13

\(y'=4x^3-4mx\Rightarrow y'\left(1\right)=4-4m\)
\(A\left(1;1-m\right)\)
Phương trình tiếp tuyến d tại A có dạng:
\(y=\left(4-4m\right)\left(x-1\right)+1-m\)
\(\Leftrightarrow\left(4-4m\right)x-y+3m-3=0\)
\(d\left(B;d\right)=\dfrac{\left|\dfrac{3}{4}\left(4-4m\right)-1+3m-3\right|}{\sqrt{\left(4-4m\right)^2+1}}=\dfrac{1}{\sqrt{\left(4-4m\right)^2+1}}\le1\)
Dấu "=" xảy ra khi và chỉ khi \(4-4m=0\Rightarrow m=1\)
y′=4x3−4mx⇒y′(1)=4−4my′=4x3−4mx⇒y′(1)=4−4m
A(1;1−m)A(1;1−m)
Phương trình tiếp tuyến d tại A có dạng:
y=(4−4m)(x−1)+1−my=(4−4m)(x−1)+1−m
⇔(4−4m)x−y+3m−3=0⇔(4−4m)x−y+3m−3=0
d(B;d)=∣∣∣34(4−4m)−1+3m−3∣∣∣√(4−4m)2+1=1√(4−4m)2+1≤1d(B;d)=|34(4−4m)−1+3m−3|(4−4m)2+1=1(4−4m)2+1≤1
Dấu "=" xảy ra khi và chỉ khi 4−4m=0⇒m=1

Vẽ hình:
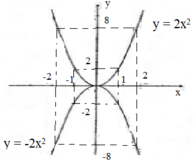
a) Nếu a > 0 thì hàm số đồng biến khi x > 0, nghịch biến khi x < 0
Với x = 0 thì hàm số đạt giá trị nhỏ nhất bằng 0. Không có giá trị nào của hàm số để đạt giá trị lớn nhất.
Nếu a < 0 thì hàm số đồng biến khi x < 0, nghịch biến khi x > 0.
Hàm số đạt giá trị lớn nhất y = 0 khi x = 0 . Không có giá trị bào của x để hàm số đạt giá trị nhỏ nhất.
b) Đồ thị hàm số y = a x 2 là đường cong (đặt tên là parabol) đi qua gốc tọa độ nhận trục tung Oy làm trục đối xứng.
Nếu a > 0 thì đồ thị nằm trên trục hoành, điểm O là điểm thấp nhất đồ thị (gọi là đỉnh parabol).
Nếu a < 0 thì đồ thị nằm bên dưới trục hoành, điểm O là điểm cao nhất của đồ thị.

- Từ các giả thiết của đề bài ta có hệ phương trình :
\(\left\{{}\begin{matrix}\dfrac{1}{9}a+\dfrac{1}{3}b+c=-\dfrac{4}{3}\\4a+2b+c=7\\-\dfrac{b}{2a}=\dfrac{1}{3}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{9}a+\dfrac{1}{3}b+c=-\dfrac{4}{3}\\4a+2b+c=7\\2a+3b=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=3\\b=-2\\c=-1\end{matrix}\right.\)
Vậy hàm số trên có dạng : \(3x^2-2x-1=0\)

a.
\(\left\{{}\begin{matrix}-\dfrac{b}{2a}=-2\\4a-2b+c=4\\c=6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}b=4a\\4a-2.4a+6=4\\c=6\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}b=4a=2\\a=\dfrac{1}{2}\\c=6\end{matrix}\right.\) \(\Rightarrow y=\dfrac{1}{2}x^2+2x+6\)
b.
\(y_{min}=y_{CT}=\dfrac{4ac-b^2}{4a}=\dfrac{4.1.1-\left(-4\right)^2}{4.1}=-3\)
Đáp án D