Trong mp Oxy cho đường thẳng (d): x – 2y – 3 = 0. Viết phương trình (d1) là ảnh của (d) qua phép đối xứng qua Δ : x + 1 = 0
A. − 7 2 x + y − 11 2 = 0
B. 7 x + y + 11 = 0
C. 7 2 x + y + 11 2 = 0
D. − 7 x + y − 11 = 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) d 1 : 3x + 2y + 6 = 0
b) Giao của d và Δ là A(2;0). Lấy B(0; −3) thuộc d. Ảnh của B qua phép đối xứng của đường thẳng Δ là B′(5;2). Khi đó d' chính là đường thẳng AB′: 2x − 3y – 4 = 0

Đáp án A
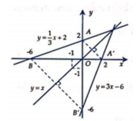
Gọi A 0 ; 2 ; B − 6 ; 0 là hai điểm thuộc đường thằng d. Gọi A' ;B' lần lượt là điểm đối xứng quả A; B qua đường thẳng y=x.
Ta có A ' = 2 ; 0 , B ' 0 ; − 6 (xem hình vẽ)
Phương trình đường thẳng A ' B ' : x 2 + y − 6 = 1 ⇔ y = 3 x − 6

a) \(d_1:3x+2y+6=0\)
b) Giao của d và \(\Delta\) là \(A\left(2;0\right)\). Lấy \(B\left(0;-3\right)\) thuộc d. Ảnh của B qua phép đối xứng qua đường thẳng \(\Delta\) là \(B'\left(5;2\right)\). Khi đó d' chính là đường thẳng AB':\(2x-3y-4=0\)

* Ta có: ĐO (A) = A’ nên O là trung điểm của AA’
Áp dụng công thức tính trung điểm ta có:
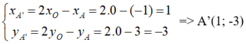
* Ta tìm ảnh của đường thẳng d qua phép đối xứng tâm O.
Do điểm O d nên qua phép đối xứng tâm O biến đường thẳng d thành đường thẳng d’// d
=> Đường thẳng d’ có dạng: x- 2y + m =0
Lấy điểm B(-3; 0)∈ d, ĐO(B) = B’∈ d’
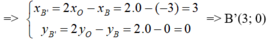
Điểm B’ (3;0) thuộc d’ nên: 3-2.0+ m = 0 ⇔ m= -3
Vậy phương trình đường thẳng d’: x- 2y – 3= 0

Giả sử M 1 = D I ( M ) và M ′ = Q O ; − 90 ο ( M 1 ) . Ta có
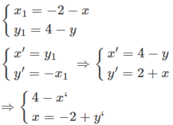
Thế (x;y) theo (x′;y′) vào phương trình d ta có:
3(y′ − 2) − (4 − x′) – 3 = 0 ⇔ x′ + 3y′ − 13 = 0
Vậy phương trình d’ là x + 3y – 13 = 0.
Đáp án C
d ∩ Δ = O ( − 1 ; − 2 )
Chọn A(1;5) ∈ d
Gọi A’ là điểm đối xứng với A qua Δ : x + 1 = 0
Đường thẳng d’đi qua A và vuông góc với Δ có phương trình: − ( y − 5 ) = 0
d’: − y + 5 = 0
d ' ∩ Δ = I ( − 1 ; 5 ) =>I là trung điểm của AA’
Đ △ : A-> A’(–3;5)
Phương trình đường thẳng (d1) đi qua O; A’: 7 2 x + y + 11 2 = 0