Trong mặt phẳng tọa độ, cho các phương trình sau. Trong các hình biểu diễn của các phương trìnhđó, hình nào có duy nhất 1 trục đối xứng:
A. y = x 2 − 2 x + 1
B. y = ( x + 1 ) 2 + ( y + 2 ) 2
C. x 2 9 + y 2 4 = 1
D. y = 2 x – 1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
(C) có tâm I(1;2) bán kính R = 3
Đ O : I → I’(–1;–2)
Phương trình đường tròn (C’): x + 1 2 + y + 2 2 = 3

Đáp án A
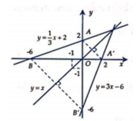
Gọi A 0 ; 2 ; B − 6 ; 0 là hai điểm thuộc đường thằng d. Gọi A' ;B' lần lượt là điểm đối xứng quả A; B qua đường thẳng y=x.
Ta có A ' = 2 ; 0 , B ' 0 ; − 6 (xem hình vẽ)
Phương trình đường thẳng A ' B ' : x 2 + y − 6 = 1 ⇔ y = 3 x − 6

Đáp án B
 Gọi
A
=
∆
∩
P
;
d
=
P
∩
Q
Gọi
A
=
∆
∩
P
;
d
=
P
∩
Q
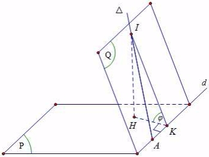
Lấy I ∈ ∆ ⇒ A ; I cố định, kẻ I H ⊥ P ; H K ⊥ d ⇒ P ; Q ^ = I K H ^ = φ
Do I A ≥ I K ⇒ sin φ = I H I K ≥ I H I A ⇒ φ m i n khi K ≡ A tức là I A ⊥ d ⇒ n Q → = u ∆ → ; u d →
Trong đó n ∆ ¯ = 1 ; - 2 ; - 2 ; u d ¯ = u ∆ ¯ ; u P ¯ = 3 ; 0 ; 3 = 3 1 ; 0 ; 1
Suy ra n Q ¯ = u ∆ ¯ ; u d ¯ = - 2 1 ; 1 ; - 1 , mặt khác (Q) chứa đường thẳng ∆ nên (Q) đi qua điểm (1;2;-1)
Do đó Q : x + y - z - 4 = 0 ⇒ A 4 ; 0 ; 0 , B ( 0 ; 4 ; 0 ) , C ( 0 ; 0 ; - 4 ) ⇒ V O . A B C = 64 6 = 32 3
Đáp án A