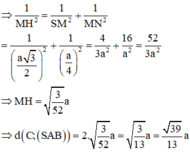Cho hình chóp S.ABC có đáy là tam giác vuông tại A, A B C ^ = 30 0 , SBC là tam giác đều cạnh a và mặt bên SBC vuông góc với mặt phẳng đáy. Tính thể tích của khối chóp S.ABC theo a.
A. 3 a 3 16 .
B. a 3 3 16 .
C. a 3 8 .
D. a 3 16 .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D.
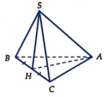
Gọi H là trung điểm của BC ![]()
∆ SBC đều cạnh bằng a nên
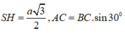
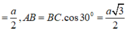
![]()
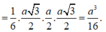

Gọi H là trung điểm của BC, suy ra \(SH\perp BC\). Mà (SBC) vuông góc với (ABC) theo giao tuyến BC, nên \(SH\perp\left(ABC\right)\)
Ta có : \(BC=a\Rightarrow SH=\frac{a\sqrt{3}}{2}\); \(AC=BC\sin30^0=\frac{a}{2}\)
\(AB=BC.\cos30^0=\frac{a\sqrt{3}}{2}\)
Do đó \(V_{S.ABC}=\frac{1}{6}SH.AB.AC=\frac{a^3}{16}\)
Tam giác ABC vuông tại A và H là trung điểm của BC nên \(HA=HB\). Mà \(SH\perp\left(ABC\right)\), suy ra \(SA=SB=a\). Gọi I là trung điểm của AB, suy ra \(SI\perp AB\)
Do đó \(SI=\sqrt{SB^2-\frac{AB^2}{4}}=\frac{a\sqrt{13}}{4}\)
Suy ra \(d\left(C;\left(SAB\right)\right)=\frac{3V_{S.ABC}}{S_{SAB}}=\frac{6V_{S.ABC}}{SI.AB}=\frac{a\sqrt{39}}{13}\)

Chọn C.
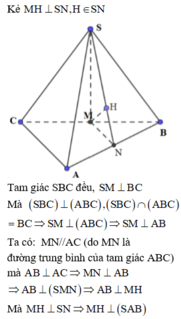
Phương pháp:
Đưa về dựng khoảng cách từ M đến (SAB) với M là trung điểm của BC.
Cách giải:
Gọi M, N lần lượt là trung điểm của BC, AB.