Tổng S = 1 + 11 + 111 + ... + 11...111 ⏟ n so 1 là
A. S = 10 81 10 n − 1 − 1 − n 9 .
B. S = 10 81 10 n − 1 + n 9 .
C. S = 1 81 10 n − 1 − n 9 .
D. S = 10 81 10 n − 1 − n 9 .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

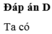
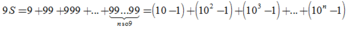
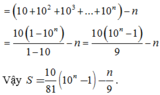

Đáp án D
Ta có 9 S = 9 + 99 + 999 + ... + 99...99 ⏟ n so 9 = 10 − 1 + 10 2 − 1 + 10 3 − 1 + ... + 10 n − 1
= 10 + 10 2 + 10 3 + ... + 10 n − n = 10 1 − 10 n 1 − 10 − n = 10 10 n − 1 9 − n
Vậy S = 10 81 10 n − 1 − n 9 .




Bài 1:
Đặt \(\underbrace{111....1}_{1009}=t\Rightarrow 9t+1=10^{1009}\)
Ta có:
\(a+b+1=\underbrace{11...11}_{1009}.10^{1009}+\underbrace{11...1}_{1009}+4.\underbrace{11....1}_{1009}+1\)
\(=t(9t+1)+t+4.t+1=9t^2+6t+1=(3t+1)^2\) là scp.
Ta có đpcm.
Bài 2:
Đặt \(\underbrace{111....1}_{n}=t\Rightarrow 9t+1=10^n\)
Ta có:
\(a+b+c+8=\underbrace{111..11}_{n}.10^n+\underbrace{111....1}_{n}+\underbrace{11...1}_{n}.10+1+6.\underbrace{111...1}_{n}+8\)
\(t(9t+1)+t+10t+1+6t+8=9t^2+18t+9\)
\(=(3t+3)^2\) là scp.
Ta có đpcm.


1) Tách S=1+(10+1)+(100+10+1)+(1000+100+10+1)+
(10000+1000+100+10+1)+...
S=10*1+9*10+8*100+7*10^3+6*10^4+
5*10^5+4*10^6+3*10^7+2*10^8+10^9
S=1234567900
2)Tổng sáu số đầu là 81 mới đúng!Nếu đây là dãy cộng thì ta có thể giải được.
Gọi hiệu 2 số liên tiếp của dãy là d.
Ta có công thức tính số hạng thứ n của dãy: a(n)=a(1)+(n-1)*d
Theo đề: a(1)+a(2)=a(1)+a(1)+(2-1)*d=2a(1)+d=7 (*)
TT:(1)+a(2)+...+a(6)=6a(1)+15*d=81(**)
từ(*) =>6a(1)+ 3*d = 21 (***)
Lấy (**)trừ(***) ta có:12*d=60 =>d=5 thế vào(*) tính được a(1)=1
Số thứ ba:a(3)=1+(3-1)*5=11
Số thứ tư:a(4)=a(3)+d=11+5=16
Than!

mình lần trước cho bạn công thức rồi mà ?![]()
![]()
Bài này hoàn toàn tương tự
* Công thức: Nếu số hạng là các chữ số n và có m số hạng:
n x [m x 100 + (m - 1) x 101 + (m - 2) x102 + ………. +2 x 10m-2 + 1 x 10m-1]
(Bạn nhớ công thức giùm mình đi)
Ta có:
A = 1 + 11 + 111 + 1111 + ... + 1111111111
A = 1 (10.1 + 9.10 + 8.100 + 7.1000 + ... + 1.1000000000)
A = 1 (10 + 90 + 800 + 7000 + 60000 + 500000 + 4000000 + 30000000 + 200000000 + 1000000000)
A = 1 . 1234567900 = 1234567900