Cho hàm số y = f ( x ) – c o s 2 x với f(x) là hàm số liên tục trên R. Trong các biểu thức dưới đây, biểu thức nào xác định f(x) thỏa mãn y ' = 1 ∀ x .
A. x + 1 2 cos 2 x
B. x - 1 2 cos 2 x
C. x − sin 2 x
D. x + sin 2 x
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Ta có
y ' = f ' x + 2 sin x . cos x = f ' x + sin 2 x
y ' = 1 ⇔ f ' x + sin 2 x = 1 ⇔ f ' x = 1 − sin 2 x ⇒ f x = x + 1 2 cos 2 x

Chọn A.
Ta có: y’ = f’(x) + 2cosxsinx = f’(x) + sin2x
y’(x) = 1 ⇔ f’(x) + sin2x = 1 ⇔ f’(x) = 1 – sin2x ⇒ f(x) = x + ½ cos2x.

Đáp án B
Phương pháp: Sử dụng phương pháp đặt ẩn phụ tính ∫ - a a f ( - x ) d x
Sử dụng công thức
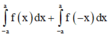
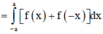
Cách giải: Đặt
![]()
Đổi cận

Khi đó ta có:
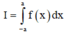
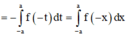

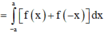
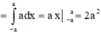
![]()