Cho x 2 = y 3 = z 5 và x + y + z = -90. Số lớn nhất trong ba số x; y; z là
A. 27
B. -27
C. -18
D. -45
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
31 tháng 12 2018
Đúng(0)
Những câu hỏi liên quan
TQ
2
CM
1 tháng 3 2017
Ta có: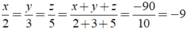 
Khi đó ta có: x = -18 ; y = -27 ; z = -45
Số lớn nhất là -18
Chọn đáp án C.
AH
Akai Haruma
Giáo viên
22 tháng 5 2021
Lời giải:
$x+y+z>\frac{1}{x}+\frac{1}{y}+\frac{1}{z}$
$\Leftrightarrow x+y+z>xy+yz+xz$ (do $xyz=1$)
$\Leftrightarrow x+y+z-xy-yz-xz>0$
$\Leftrightarrow xyz+x+y+z-xy-yz-xz-1>0$
$\Leftrightarrow (x-xy)+(y+z-yz-1)+(xyz-xz)>0$
$\Leftrightarrow x(1-y)+(1-y)(z-1)-xz(1-y)>0$
$\Leftrightarrow (1-y)(x+z-1-xz)>0$
$\Leftrightarrow (1-y)(1-z)(x-1)>0$
$\Leftrightarrow (1-y)(1-z)(1-x)<0(*)$
Nếu trong 3 số $x,y,z$ đều nhỏ hơn $1$ thì $(1-y)(1-z)(1-x)>0$ (mâu thuẫn với $(*)$)
Do đó trong 3 số có ít nhất 1 số lớn hơn $1$.
25 tháng 2 2020
Vai trò \(x,y,z\)như nhau không mất tính tổng quát ta giả sử \(x\ge y\ge z\)
Nếu \(x< 2\)thì \(xyz< 2\cdot2\cdot z=4z=z+3z< 2+3z\le2+x+y+z\)(mâu thuẫn)
Vậy \(x\ge2\)
Nếu \(z>2\)thì \(xyz>x\cdot2\cdot2=4x=x+3x>2+3x\ge2+x+y+z\)(mâu thuẫn)
Vậy \(z\le2\)
Nghĩa là có ít nhất 1 số không nhỏ hơn 2 và ít nhất 1 số không lớn hơn 2
22 tháng 2 2020
Ta giả sử 3 số đều =2
=>\(\frac{1}{3}+\frac{1}{3}+\frac{1}{3}=1\)(Đúng)
=>đpcm
P/s : nhanh gọn lẹ :))
10 tháng 3 2020
Đặt \(A=\frac{1}{x+1}+\frac{1}{y+1}+\frac{1}{z+1}=1\)
Không mất tính tổng quát giả sử:
\(\frac{1}{x+1}< \frac{1}{y+1}< \frac{1}{z+1}\)
Ta có
+) \(A>\frac{3}{1+x}\Leftrightarrow1>\frac{3}{1+x}\)
\(\Leftrightarrow\frac{1}{3}>\frac{1}{x+1}\Leftrightarrow x+1>3\)
<=> x>2(1)
+) \(A< \frac{3}{1+z}\Leftrightarrow1< \frac{3}{1+z}\Leftrightarrow\frac{1}{3}< \frac{1}{1+z}\Leftrightarrow1+z< 3\Leftrightarrow x< 2\)(2)
Từ (1) (2) => ĐPCM
7 tháng 9 2021
\(4=x+y+z\ge3\sqrt[3]{xyz}\Leftrightarrow\sqrt[3]{xyz}\le\dfrac{4}{3}\Leftrightarrow xyz\le\dfrac{64}{27}\)(BĐT cauchy)
Dấu \("="\Leftrightarrow x=y=z=\dfrac{4}{3}\)
AH
Akai Haruma
Giáo viên
7 tháng 9 2021
Lời giải:
Áp dụng BĐT AM-GM:
$xy\le \frac{(x+y)^2}{4}=\frac{(4-z)^2}{4}$
$\Rightarrow H\leq \frac{z(4-z)^2}{4}$
Tiếp tục áp dụng BĐT AM-GM:
$z(4-z)\leq \frac{(z+4-z)^2}{4}=4$
$4-z\leq 2$ do $z\geq 2$
$\Rightarrow \frac{z(4-z)^2}{4}\leq \frac{4.2}{4}=2$
Hay $H\leq 2$
Vậy $H_{\max}=2$ khi $(x,y,z)=(1,1,2)$
