Chứng minh rằng G = 8 8 + 2 20 ⋮ 17
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
21 tháng 6 2018
Đúng(0)
Những câu hỏi liên quan
6 tháng 2 2015
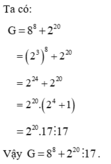
Ta có 88 + 220 = (23)8 + 220
= 224 + 220
= 220.(24 + 1)
= 220.(16 + 1)
= 220.17 chia hết cho 17
NT
1
VT
1 tháng 7 2015
(8^8+2^20)=(2^24+2^20)=2^20.(2^4+1)=2^20.17. Suy ra 2^20 chia het cho 17. Vay (8^8+2^20) chia het cho 17.
5 tháng 7 2015
88 + 220 = (23)8 + 220 = 224 + 220 = 220.(24 + 1) = 220.17 chia hết cho 17
MT
5 tháng 7 2015
8^8+2^20
=(23)8+220
=224+220
=220.(24+1)
=220.17
=>220.17 chia hết cho 17
vậy 8^8+2^20 chia hết cho 17
NN
14 tháng 7 2017
Tham khảo:
Câu hỏi của Trần Ngọc Quốc Nam - Toán lớp 6 - Học toán với OnlineMath (câu G)
~ Học tốt!!! ~
NN
14 tháng 7 2017
Giải:
\(8^8+2^{20}⋮17.\)
\(=\left(2^3\right)^8+2^{20}.\)
\(=2^{24}+2^{20}.\)
\(=2^{20}.2^4+2^{20}.\)
\(=2^{20}.2^4+2^{20}.1.\)
\(=2^{20}\left(2^4+1\right).\)
\(=2^{20}\left(16+1\right).\)
\(=2^{20}.17⋮17.\)
\(\Rightarrowđpcm.\)
~ Học tốt!!! ~
HP
8 tháng 11 2015
\(8^8+2^{20}=\left(2^3\right)^8+2^{20}=2^{24}+2^{20}=2^{20}\left(2^4+1\right)=2^{20}.17\) chia hết cho 17(đpcm)
PT
25 tháng 11 2015
Ta có: 8^8+2^20=(2^3)^8+2^20
=2^24+2^20
=2^20(2^4+1)
=2^20 * 17 chia hết cho 17
Vậy 8^8+2^20 chia hết cho 17 (Điều phải chứng minh)
TT
5
N
13 tháng 10 2018
\(=\left(2^3\right)^8+2^{20}\)
\(=2^{24}+2^{20}\)
\(=2^{20}.\left(2^4+1\right)\)\(=2^{20}.17⋮17\)
Vậy ...
13 tháng 10 2018
88 + 220
= (23)8 + 220
= 224 + 220
= 220.24 + 220.1
= 220(24 + 1)
= 220.17 ⋮ 17 (đpcm)
